
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর ষষ্ঠ অধ্যায় সর্বসমতা ও সদৃশতা, সম্পর্কে।
সর্বসমতা ও সদৃশতা (congruence and similarity)
আমরা এই অধ্যায়ে শিখন ফলাফলে কতগুলো সূত্র বা শর্ত জানব যার ভিত্তিতে আমরা সর্বসমতা ও সদৃশতা কেন হয় বা হয়ে থাকে তা জানব। তার ভিত্তিতে আমরা মূল কাজসমূহ সমাধান করব যা এই অধ্যায়ের শেষে প্রদত্ত আছে।
ত্রিভুজের সর্বসমতা (congruence) এর শর্তঃ
- দুইটি ত্রিভুজের যেকোনো দুই বাহু এবং তাদের মধবর্তী কোণ সমান হলে ত্রিভুজ দুইটি সর্বসম হবে।
- দুইটি ত্রিভুজের তিনটি বাহুই সমান হলে ত্রিভুজ দুইটি সর্বসম হবে।
- দুইটি ত্রিভুজের যেকোনো দুই কোণ এবং কোণ সংলগ্ন বাহু সমান হলে ত্রিভুজ দুইটি সর্বসম হবে।
ত্রিভুজের সদৃশতা (similarity) এর শর্তঃ
- যদি একটি ত্রিভুজের তিন বাহু অপর একটি ত্রিভুজের তিন বাহুর সমানুপাতিক হয়, তাহলে ত্রিভুজ দুইটি সদৃশ হবে।
- যদি একটি ত্রিভুজের দুই বাহু অপর একটি ত্রিভুজের দুই বাহুর সমানুপাতিক হয় এবং তাদের মধ্যেকার কোণগুলো যদি পরস্পর সমান হয়, তাহলে ত্রিভুজ দুইটি সদৃশ হবে।
- যদি একটি ত্রিভুজের দুইটি কোণ অপর একটি ত্রিভুজের দুইটি কোণের সমান হয়, তাহলে ত্রিভুজ দুইটি সদৃশ হবে।
চতুর্ভুজের সদৃশতা এর শর্তঃ
- দুইটি চতুর্ভুজের অনুরূপ বাহুগুলো সমানুপাতিক এবং একটি অনুরূপ কোণ সমান হলে চতুর্ভুজ দুইটি সদৃশ।
অনুশীলনী এর একক কাজঃ
১। চিত্রে ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC। w চিহ্নিত কোণের পরিমাপ কত হবে?
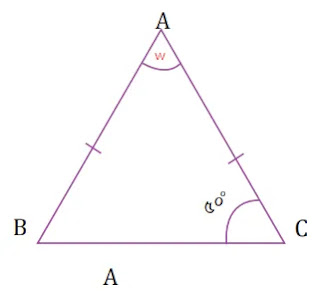
সমাধানঃ
দেওয়া আছে,
ত্রিভুজ ABC এর AB=AC.
তাহলে,
∠ABC=∠ACB [যেহেতু, সমদ্বিবাহু ত্রিভুজ এর সমান সমান কোণের বিপরীত কোণদ্বয়ও সমান]
বা, ∠ABC = ৫০° [চিত্র অনুসারে মান বসিয়ে]
আবার, আমরা জানি,
ত্রিভুজের তিন কোণের সমষ্টি = ২ সমকোণ
অতএব,
ত্রিভুজ ABC এর ক্ষেত্রে,
∠ABC+∠ACB+∠BAC = ২ সমকোণ
বা, ৫০° + ৫০°+ ∠BAC = ১৮০°
বা, ১০০° + ∠BAC = ১৮০°
বা, ∠BAC = ১৮০° – ১০০°
বা, ∠BAC = ৮০°
বা, ∠w = ৮০°
অতএব, w চিহ্নিত কোণের পরিমাণ ৮০°
বিঃদ্রঃ চিত্রে w চিহ্নিত কোণের পরিমাণ উল্লেখ নেই এবং যে কোণের মান ৫০° দেওয়া আছে সেই অনুসারে প্রাপ্ত কোণ ৮০° হলেও চিত্রের মাপে বিভ্রান্ত হতে হয় যাই হোক উপরের সমাধান গাণিতিক, পরিমাপগত নয়]
২। চিত্রে ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC। y চিহ্নিত কোণের পরিমাপ কত হবে?
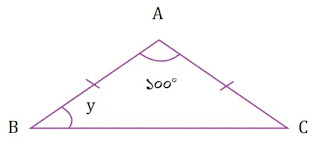
সমাধানঃ
ত্রিভুজের তিন কোণের সমষ্টি সূত্র অনুসারে আমরা লিখতে পারি,
ΔABC এর
∠ABC+∠ACB+∠BAC = ২ সমকোণ
বা, ∠ABC+∠ACB+১০০° = ১৮০°
বা, ∠ABC+∠ACB = ১৮০°-১০০°
বা, ∠ABC+∠ACB = ৮০°
এখন শর্ত অনুসারে, AB=AC
তাহলে, ∠ABC = ∠ACB [[যেহেতু, সমদ্বিবাহু ত্রিভুজ এর সমান সমান কোণের বিপরীত কোণদ্বয়ও সমান]
এখন,
∠ABC+∠ACB = ৮০°
বা, ∠ABC+∠ACB = ৮০°
বা, ∠ABC+∠ABC = ৮০°
বা, ২∠ABC = ৮০°
বা, ∠ABC = ৮০°/২
বা, ∠ABC = ৪০°
বা, y = ৪০°
অতএব, y চিহ্নিত কোণের পরিমান ৪০°।
৩। প্রদত্ত চিত্রে AB ও DE পরস্পর সমান্তরাল। চিত্রে বর্ণিত তথ্য ব্যবহার করে নিচের প্রশ্নগুলোর উত্তর দাও।
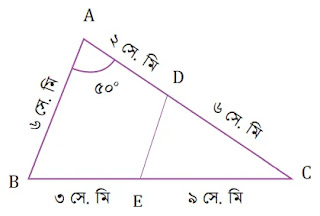
(ক) কোণ ADE এর মান কত?
(খ) চিত্রে দুইটি সদৃশ ত্রিভুজ আছে, তাদেরকে খজেুঁ বের করো। কেন তারা সদৃশ হবে?
(গ) সদৃশ ত্রিভুজের বৈশিষ্ট্য ব্যবহার করে DE এর দৈর্ঘ্য বের করো।
সমাধানঃ
(ক)
চিত্রে, AB ও DE পরস্পর সমান্তরাল এবং AC তাদের ছেদক।
তাহলে,
∠BAC = ∠EDC [অনুরুপ কোণ]
বা, ∠EDC = ∠BAC
বা, ∠EDC = ৫০°
আবার,
আমরা জানি,
এক সরল কোণ = ১৮০°
বা, ∠ADC = ১৮০°
বা, ∠ADE+∠EDC = ১৮০°
বা, ∠ADE + ৫০° = ১৮০° [মান বসিয়ে]
বা, ∠ADE = ১৮০° – ৫০°
বা, ∠ADE = ১৩০°
অতএব, কোণ ADE এর মান ১৩০°।
(খ)
চিত্রে দুইটি সদৃশ ত্রিভুজ আছে, তারা হলোঃ ΔABC ও ΔDEC.
ΔABC ও ΔDEC এর সদৃশ কেনঃ
আমরা জানি,
দুইটি ত্রিভুজ সদৃশ হবে যদি একটি ত্রিভুজের দুই বাহু অপর একটি ত্রিভুজের দুই বাহুর সমানুপাতিক হয় এবং তাদের মধ্যেকার কোণগুলো যদি পরস্পর সমান হয়।
চিত্র অনুসারে,
AC : DC = (6+2) : 6 = 8 : 6 = 4 : 3
আবার,
BC : EC = (9+3) : 9 = 12 : 9 = 4 : 3
এবং এদের মধ্যবর্তী কোণ ∠BCA = ∠ECD
অতএব, ΔABC ও ΔDEC সদৃশ [কেন দেখানো হলো]
(গ)
সদৃশ ত্রিভুজের বৈশিষ্ট্য ব্যবহার করে DE এর দৈর্ঘ্য নির্ণয়ঃ
খ হতে আমরা পাই,
ΔABC ও ΔDEC সদৃশ।
আবার আমরা জানি,
যদি একটি ত্রিভুজের তিন বাহু অপর একটি ত্রিভুজের তিন বাহুর সমানুপাতিক হয়, তাহলে ত্রিভুজ দুইটি সদৃশ হবে।
তাহলে, ΔABC তিন বাহু, ΔDEC তিন বাহু সমানুপাতিক হবে।
চিত্র অনুসারে,
AC : DC = (6+2) : 6 = 8 : 6 = 4 : 3
BC : EC = (9+3) : 9 = 12 : 9 = 4 : 3
তাহলে,
AB : DE = 4 : 3
বা, 6 : DE = 4 : 3
বা, 6/DE = 4/3
বা, 4DE = 6×3
বা, 4DE = 18
বা, DE = 18/4
বা, DE = 9/2
বা, DE = 4.5
অতএব, DE এর দৈর্ঘ্য 4.5 সেমি।
পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

