এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর অষ্টম অধ্যায় চলো বৃত্ত চিনি, সম্পর্কে।

চলো বৃত্ত চিনি

চলো বৃত্ত চিনি হলো ২০২৩ এর সপ্তম শ্রেণির গণিত পাঠ্যবইয়ের অষ্টম অধ্যায় এর নাম। এই অধ্যায়ে বৃত্ত সম্পর্কে আলোচনা করা হয়েছে। নিচে কিছু বস্তুর ছবি দেয়া হয়েছে। পাঠ্যবইয়ে নিচের আকৃতিগুলো চেনানোর মাধ্যমে চলো বৃত্ত চিনি এর সূচনা করা হয়েছে। আমরা পাঠ্যবইয়ের সমস্যাগুলো সমাধান করবো। তাহলে শুরু করা যাক-

দলগত কাজ: বৃত্তাকার বস্তুর নাম লেখার প্রতিযোগিতা। সময়ঃ ৫ মিনিট। দলের প্রত্যেকে নিজ নিজ খাতায় বৃত্তাকার বস্তুর নাম লিখবে। যে সবচেয়ে বেশি নাম লিখতে পারবে, সে জয়লাভ করবে।

সমাধানঃ

কে জয়লাভ করবে তাহা শিক্ষক বিচার করবেন। আমরা এখানে শুধু কিছু বৃত্তাকার বস্তুর নাম তুলে ধরলাম।

• চাকা
• ডিস্ক
• বোতাম
• মেডেল বা পদক
• দেয়াল ঘড়ি
• সিডি
• লেন্স
• পিজ্জা
• প্যানকেক
• চাঁদ
• সূর্য
• বৃত্তাকার পথ
• প্লেট
• বাটি
• আপেল
• বল
• সাইকেল চাকা
• চুড়ি
• কয়েন
• কন্টাক্ট লেন্স
• জারের ঢাকনা
• প্লেট
• সূর্যমুখী
• কয়ল
• গ্লোব ইত্যাদি।

দলগত কাজ:

কতগুলো ছোট ছোট দলে বিভক্ত হয়ে বিভিন্ন দৈর্ঘ্যের দড়ি ব্যবহার করে মাটিতে দিশার মতো বৃত্ত তৈরি করো। দলগুলোর নাম দাও। প্রত্যেক দলের তৈরি করা বৃত্তগুলো পর্যবেক্ষণ করো এবং নিচের প্রশ্নগুলোর উত্তর খাতায় লিখ।

1. কোন দল সবচেয়ে ছোট বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য কত মিটার?
2. কোন দল সবচেয়ে বড় বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য কত মিটার?
3. দড়ির দৈর্ঘ্য বেশি হলে বৃত্তটির আকার কীরূপ হবে, যুক্তিসহ ব্যাখ্যা করো।

সমাধানঃ

আমাদের ছোট ছোট দলে বিভক্ত দলগুলোর নাম ও ব্যবহৃত দড়ির দৈর্ঘ্য হলোঃ

দলের নাম	দড়ির দৈর্ঘ্য (মিটার)
অর্জুন দল	১ মিটার
শাপলা দল	১.৫ মিটার
জবা দল	২ মিটার
আপেল দল	২.৫ মিটার

প্রশ্নগুলোর উত্তরঃ

1. অর্জুন দল সবচেয়ে ছোট বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য ১ মিটার।
2. আপেল দল সবচেয়ে বড় বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য ২.৫ মিটার।
3. দড়ির দৈর্ঘ্য যত বেশি হবে বৃত্তের আকার তত বড় হবে। ব্যাখ্যাঃ এখানে দড়ির দৈর্ঘ্য বৃত্তের ব্যাসার্ধ হিসেবে কাজ করে আর আমরা জানি বৃত্তের ব্যাসার্ধ যত বেশি হবে বৃত্তটিও তত বড় হবে।

একক কাজ: প্রত্যেকেই মীরার মতো চূড়ি ব্যবহার করে বৃত্তাকার কাগজ কেটে কেন্দ্র নির্ণয় করো। চূড়ির পরিবর্তে কাপ বা গ্লাস বা অন্যকোনো বস্তু দ্বারাও বৃত্তাকার কাগজ কেটে নিতে পারবে। তাছাড়া কেন্দ্র নির্ণয়ে অন্য কোনো পদ্ধতিও ব্যবহার করতে পারবে।

সমাধানঃ

আমি আমার খাতায় একটি চুড়ি বসিয়ে চুড়ির মাপে কাগজ কেটে নেই। ফলে একটি কাগজের বৃত্ত পেয়ে গেলাম।

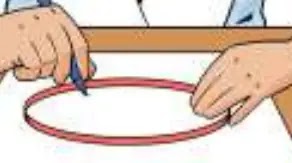
কাগজের বৃত্তের কেন্দ্র নির্ণয়ঃ

কাগজটিকে প্রথমে চিত্রের মত করে দুইটি ভাঁজ দিয়ে সমান চার ভাগে ভাঁজ করি। দুইটি ভাঁজের ছেদবিন্দু চিহ্নিত করি। তাহলে উক্ত ছেদবিন্দুটিই হলো কাগজের বৃত্তের কেন্দ্র।

দলগত কাজ:

চিত্রের মতো কাগজে একটি বৃত্ত আঁক। তারপর বৃত্তের উপর কতগুলো পিন বসিয়ে নাও। লক্ষ রাখবে, ব্যাসের দুই প্রান্তে বৃত্তের উপর যেন দুইটি পিন থাকে। রাবার দিয়ে চিত্রের মতো ব্যাস ও জ্যা তৈরি করো। প্রয়োজনে পিনগুলোর গোড়ায় বিন্দু দিয়ে চিহ্নিত করো। তারপর বৃত্তের ব্যাসার্ধ, জ্যা, উপচাপ, অধিচাপ, অর্ধবৃত্তসহ সকল অঙ্গ নিয়ে সকলে আলোচনা করো। স্কেল ও সূতা ব্যবহার করে বৃত্তের ব্যাসার্ধ, ব্যাস, জ্যা, বৃত্তচাপ মেপে খাতায় লিখ। এবার নিচের প্রশ্নগুলোর উত্তর খজেুঁ দেখোঃ

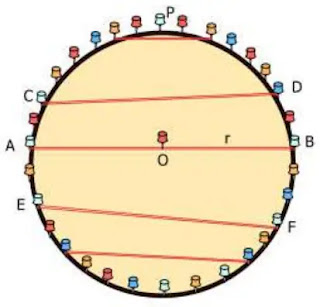
(১) বৃত্তের ব্যাস ও ব্যাসার্ধের মর্ধ্যে সম্পর্ক কী? 

(২) বৃত্তের কোন জ্যা-টি সবচেয়ে বড়?

(৩) সবচেয়ে বড় জ্যাটিকে আমরা কী বলে থাকি?

(৪) বৃত্তের ব্যাস বৃত্তকে দুই ভাগে ভাগ করেছে তাদের দৈর্ঘ্য কীরূপ? 

(৫) বৃত্তের ব্যাস দ্বারা সৃষ্ট চাপ দুইটির প্রত্যেকটিকে কী বলা হয়?

সমাধানঃ

চিত্রের মতো কাগজে একটি বৃত্ত আঁকলাম। তারপর বৃত্তের উপর কতগুলো পিন বসিয়ে নিলাম। ব্যাস বরাবর দুই প্রান্তে দুইটি পিন রাখলাম। রাবার দিয়ে চিত্রের মতো ব্যাস ও জ্যা তৈরি করলাম। এবং পিনগুলোর গোড়ায় বিন্দু লিখে চিহ্নিত করলাম।

স্কেল ও সূতা ব্যবহার করে বৃত্তের ব্যাসার্ধ, ব্যাস, জ্যা, বৃত্তচাপ মেপে খাতায় লিখলাম। মাপগুলো নিন্মরুপঃ

ব্যাসার্ধ	২ সেমি
ব্যাস	৪ সেমি
জ্যা	৩ সেমি, ৩.২ সেমি, ২ সেমি, ১.৪ সেমি, ০.৫ সেমি।
বৃত্তচাপ	৩ সেমি, ৩.২ সেমি, ২.২ সেমি ইত্যাদি

(১) বৃত্তের ব্যাস ও ব্যাসার্ধের মধ্য সম্পর্কঃ বৃত্তের ব্যাস তার ব্যাসার্ধের দ্বিগুণ।

(২) বৃত্তের যে জ্যা-টি বৃত্তের কেন্দ্র দিয়ে যায় সেটি সবচেয়ে বড় জ্যা। উল্লেখ্য ব্যাসও একটি জ্যা অর্থাৎ ব্যাসই বৃত্তের সবচেয়ে বড় জ্যা।

(৩) সবচেয়ে বড় জ্যাটিকে আমরা ব্যাস বলে থাকি।

(৪)বৃত্তের ব্যাস বৃত্তকে দুই ভাগে ভাগ করেছে তাদের দৈর্ঘ্য সমান।

(৫)বৃত্তের ব্যাস দ্বারা সৃষ্ট চাপ দুইটির প্রত্যেকটিকে অর্ধচাপ বলে।

একক কাজ:

১. কাগজ কেটে নিচের চিত্রের মতো বৃত্তের কেন্দ্র, ব্যাসার্ধ, জ্যা এবং পরিধি তৈরি করো।

সমাধানঃ

চিত্র অনুসারে নিজে চেষ্টা করো।

২. পেন্সিল কম্পাসের সাহায্যে খাতায় বিভিন্ন মাপের কয়েকটি বৃত্ত আঁক। বৃত্তগুলোর কেন্দ্র চিহ্নিত করো। বৃত্তগুলোর উপরে বিভিন্ন জায়গায় কয়েকটি বিন্দু নিয়ে কেন্দ্র থেকে বিন্দুগুলো পর্যন্ত রেখাংশগুলো আঁক। প্রতিটি বৃত্তের কেন্দ্রগামী জ্যা বা ব্যাস আঁক। এবার খাতায় নিচের ছক বা সারণিটি তৈরি করো। প্রতিটি বৃত্তের ব্যাসার্ধ কেন্দ্রগামী জ্যা বা ব্যাসের দৈর্ঘ্য পরিমাপ করে সারণিটি পূরণ করো এবং সহপাঠির সাথে ফলাফল নিয়ে আলোচনা করো।

সমাধানঃ

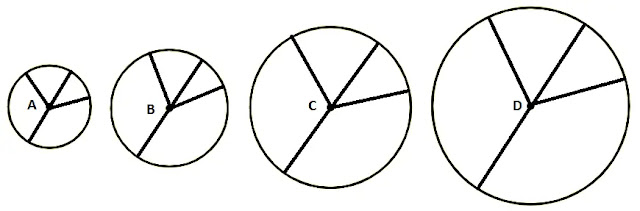
পেন্সিল কম্পাসের সাহায্যে চারটি বৃত্ত আঁকলাম। বৃত্তচারটির কেন্দ্র যথাক্রমে A, B, C, D চিহ্নিত করলাম। বৃত্তের উপরে বিভিন্ন বিন্দু নিয়ে কেন্দ্র থেকে বিন্দুগুলো পর্যন্ত রেখাংশগুলো আঁকলাম এবং তার সাথে প্রত্যেকটি বৃত্তে ব্যাস আঁকলাম। অতপর বৃত্তগুলোর ব্যাসার্ধ ও ব্যাসের দৈর্ঘ্য পরিমাপ করে প্রদত্ত সারণিটি পুরন করে সহপাঠির সাথে ফলাফল নিয়ে আলোচনা করলাম।

পুরণকৃত সারণি ও ফলাফল নিন্মরুপঃ

বৃত্ত	কেন্দ্র থেকে বৃত্তের দৈর্ঘ্য বা ব্যাসার্ধ	কেন্দ্রগামী জ্যায়ের দৈর্ঘ্য বা ব্যাসের দৈর্ঘ্য	ফলাফল পর্যবেক্ষন করে বৃত্তের ব্যাসার্ধ ও কেন্দ্রগামী জ্যা বা ব্যাস এর মধ্যকার সম্পর্ক বর্ণনা
১.	১ সেমি	২ সেমি	ব্যাস = ২xব্যাসার্ধ
২.	১.৫ সেমি	৩ সেমি	ব্যাস = ২xব্যাসার্ধ
৩.	২ সেমি	৪ সেমি	ব্যাস = ২xব্যাসার্ধ
৪.	২.৫ সেমি	৫ সেমি	ব্যাস = ২xব্যাসার্ধ

৩. কাগজ কেটে ৩ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট পাঁচটি বৃত্ত তৈরি করো। বৃত্তগুলোকে নিচের চিত্রের মতো সাজিয়ে কেন্দ্রগুলো যোগ করে ইংরেজি বর্ণ W আকৃতিটি বানাও। এবার A থেকে B পর্যন্ত দৈর্ঘ্য নির্ণয় করো। C কেন্দ্রবিশিষ্ট বৃত্তটির চার পাশে এভাবে সর্বোচ্চ কয়টি বৃত্ত সাজানো যাবে?

সমাধানঃ

কাগজ কেটে ৩ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট পাঁচটি বৃত্ত তৈরি করলাম। বৃত্তগুলোকে নিচের চিত্রের মতো সাজিয়ে কেন্দ্রগুলো যোগ করে ইংরেজি বর্ণ W আকৃতিটি বানালাম।

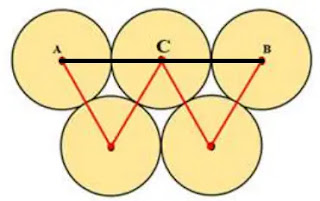
A থেকে B পর্যন্ত দৈর্ঘ্য নির্ণয়ঃ

চিত্রে, A, C ও B কেন্দ্রবিশিষ্ট তিনটি বৃত্ত পাশাপাশি অবস্থান করছে যেখানে প্রত্যেকটি বৃত্তের ব্যসার্ধ হলো ৩ সেমি।

তাহলে,

A থেকে C এর দূরত্ব

= A কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ + C কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ

= ৩ সেমি + ৩ সেমি

= ৬ সেমি।

আবার,

C থেকে B এর দূরত্ব

= C কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ + B কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ

= ৩ সেমি + ৩ সেমি

= ৬ সেমি।

অতএব, A থেকে B এর দূরত্ব = ৬ সেমি + ৬ সেমি = ১২ সেমি।

C কেন্দ্রবিশিষ্ট বৃত্তটির চার পাশে এভাবে সর্বোচ্চ যতগুলি বৃত্ত সাজানো যাবে তাহা নির্ণয়:

চিত্র অনুসারে, C এর বাম পাশে একটি বৃত্ত আছে এবং সেই অনুসারে ডানপাশেও একটি বৃত্ত আছে।

অর্থাৎ, বাম ও ডান পাশে মোট বৃত্তের সংখ্যা ২টি।

আবার,

C এর নিচে ২টি বৃত্ত আছে, সেই অনুসারে C এর উপরেও ২টি বৃত্ত একইভাবে সাজানো যাবে।

তাহলে, C এর উপরে ও নিচে মোট বৃত্ত সাজানো যাবে ২+২ টি = ৪টি।

অতএব,

C এর চারপাশে অর্থাৎডানে-বামে এবং উপরে নিচে মোট বৃত্ত সাজানো যাবে

= ২টি + ৪টি

= ৬টি।

বৃত্তের পরিধি  – ৮ম অধ্যায় ( ১৭১ – ১৭৬ পৃষ্ঠা)

 

বৃত্তের পরিধি

দলগতকাজ:পাই মডেল তৈরিঃ  একটি শোলার বোর্ড বা মোটা কাগজের যেকোনো বোর্ডে বৃত্তাকার মডেল তৈরি করো। যেহেতু বৃত্ত একটি আবদ্ধ বক্ররেখা তাই এটি স্কেল দ্বারা  সরাসরি মাপা সম্ভব নয়। সেজন্য একটি সূতা বা চিকন দড়ির একপ্রান্ত নিচের চিত্রের মতো বৃত্তটির উপরস্থ  একটি পিনের সাথে বেঁধে সূতা বা দড়িটিকে বৃত্তটির উপর দিয়ে ঘুরিয়ে আনো যেন সূতাটি পিনে বাঁধা প্রান্তটিকে স্পর্শ করে।  সূতার স্পর্শ বিন্দু বরাবর চিহ্নিত করো এবং কাঁচি বা ব্লেড দিয়ে কেটে ফেলো। এবার সূতার কাঁটা অংশটি সোজা করে স্কেল দিয়ে মেপে নাও এবং খাতায় লিখে রাখো যা হলো বৃত্তের পরিধি। এবার বৃত্তক্ষেত্রটির ব্যাস মেপে নাও। ভিন্ন ভিন্ন ব্যাসার্ধের বৃত্তক্ষেত্র তৈরি করে দলের সকলেরই নির্দেশনা মতো কাজটি করো। খাতায় নিচের মতো একটি সারণি তৈরি করো। সারণিতে দলের সদস্যদের নাম লিখে নিজ নিজ পরিমাপগুলো লিপিবদ্ধ করে হিসাব করো।

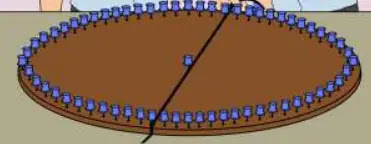
সমাধানঃ

আমরা প্রত্যেকে বৃত্তাকার মডেল তৈরি করে সুতা দিয়ে বৃত্তের পরিধি ও ব্যাস মেপে নিয়ে প্রদত্ত সারনিতে পরিমাপগুলো লিপিবদ্ধ করে হিসাব করলাম।

নাম	বৃত্তের ব্যাসার্ধ	বৃত্তের ব্যাস	বৃত্তের পরিধি	পরিধি ও ব্যাসের অনুপাত
নিলীমা	১	২	৬.২৮	৬.২৮ : ২ = ৩.১৪ : ১
শাহেদ	১.৫	৩	৯.৪২	৯.৪২ : ৩ = ৩.১৪ : ১
রঞ্জনা	২	৪	১২.৫৬	১২.৫৬ : ৪ = ৩.১৪ : ১
প্রতীক	২.৫	৫	১৫.৭০	১৫.৭০ : ৫ = ৩.১৪ : ১
বাবুল	৩	৬	১৮.৮৪	১৮.৮৪ : ৬ = ৩.১৪ : ১

শিখন ফলাফলঃ

বৃত্তের পরিধি = c ও বৃত্তের ব্যাসার্ধ = r হলে,

c = 2πr যেখানে π এর মান 3.1415 (প্রায়)।

পাই দিবসঃ ১৪ মার্চ।

মার্কিনযুক্তরাষ্ট্রে৩/২৭/২০২৩মানেহচ্ছে২৭মার্চ২০২৩  

আর এজন্যই পাইয়ের মান ৩.১৪১৫৯২ থেকে প্রথম ৩টি 

 অঙ্ক নিয়ে ৩/১৪ কে তারিখ লেখার নিয়মে ১৪ মার্চ যাকে 

পাই দিবস হিসেবে পালন করা হয়।

১. প্রথমে দিন, তারপর মাস তারপর বছর এভাবে 

 হিসাব করলে কোন তারিখ ‘পাই দিবস’ হতে পারতো?

উত্তরঃ ৩/১৪/২০২৩

২. আচ্ছা, ওই তারিখে কি ‘পাই দিবস’ 

 উদযাপন করা সম্ভব? তোমার কি মনে হয়?

উত্তরঃ না, সম্ভব নয়। কারণ মাঝের সংখ্যা ১৪ কে 

মাস ধরা হয়েছে, কিন্তু ১৪তম মাস হতে পারে না কারণ বছরে মাসের সংখ্যা ১২।

৩. যদি ইংরেজী মাসের (জানুয়ারি, ফেব্রুয়ারী,  

মার্চ ইত্যাদি) বদলে বাংলা মাস (বৈশাখ, জৈষ্ঠ্য,  

আষাঢ়, শ্রাবণ ইত্যাদি) দিয়ে চিন্তা করা হয়  

তাহলে কোন তারিখগুলি ‘পাই দিবস’ হতে  

পারতো বলে তুমি মনে করো?

উত্তরঃ ১৪ই আষাঢ় হতে পারতো বলে আমি মনে করি।

শিখন ফলাফলঃ ২০১৯ সালে UNESCO তাদের ৪০ 

 তম সাধারণ অধিবেশনে ‘১৪ মার্চ’কে 

 ‘আন্তর্জাতি ক গণিত দিবস (International Day

 of Mathematics)’ ঘোষণা করে।

একক কাজ:

নিচের ছকটি খাতায় তৈরি  

করে নির্দেশনা অনুসারে পূরণ করো।

সমাধানঃ

প্রদত্ত ছকটি পূরণ করে নিচে দেওয়া হলোঃ

ক্রমিক নম্বর	বৃত্তের ব্যাসার্ধ (r)	বৃত্তের ব্যাস (d)	বৃত্তের পরিধি (c)	c/d
১	7 সেন্টিমিটার	14 সেন্টিমিটার	43.9824 সেন্টিমিটার	3.1416
২	14 সেন্টিমিটার	28 সেন্টিমিটার	87.9648 সেন্টিমিটার	3.1416
৩	24.51 সেন্টিমিটার	49.02 সেন্টিমিটার	154 সেন্টিমিটার	3.1416
৪	5.2 সেন্টিমিটার	10.4 সেন্টিমিটার	32.6726 সেন্টিমিটার	3.1416
৫	6 সেন্টিমিটার	12 সেন্টিমিটার	37.6992	3.1416
৬	19.9898 সেন্টিমিটার	39.9796 সেন্টিমিটার	125.6 সেন্টিমিটার	3.1416

এখানে ব্যবহৃত সূত্রসমূহঃ

1. d=2r; c=2πr

2. r=^d/₂; c=2πr

3. d=^c/_π; r=^d/₂

4. d=2r; c=2πr

5. r=^d/₂; c=2πr

6. d=^c/_π; r=^d/₂

প্রশ্নঃ একটি বৃত্তাকার পার্কের ব্যাস ও পরিধির 

 পার্থক্য 90 মিটার। পার্কটির ব্যাসার্ধ নির্ণয় করো।

সমাধানঃ

মনে করি, বৃত্তাকার পার্কটির ব্যাসার্ধ = r মিটার।

তাহলে, বৃত্তাকার পার্কের ব্যাস = 2r মিটার এবং পরিধি = 2πr মিটার।

প্রশ্নমতে,

2πr – 2r = 90

বা, 2r(π-1) = 90

বা, r(π-1) = ⁹⁰/₂

বা, r(3.1416-1) = 45 [π এর মান 3.1416 বসিয়ে]

বা, rx2.1416 = 45

বা, r = ⁴⁵/_2.1416

বা, r = 21.01 (প্রায়)

অর্থাৎ, পার্কটির ব্যাসার্ধ 21.01 মিটার (প্রায়)।

প্রশ্নঃ একটি গাড়ির সামনের চাকার ব্যাস

  28 সেন্টিমিটার এবং  

পিছনের চাকার 

 ব্যাস 35 সেন্টিমিটার। 88 মিটার পথ যেতে সামনের 

 চাকা পিছনের চাকা অপেক্ষা কত বার বেশি ঘুরবে?

সমাধানঃ

দেওয়া আছে,

গাড়ির সামনের চাকার ব্যাস 28 সেন্টিমিটার

তাহলে, গাড়ির সামনের চাকার পরিধি

= 28π  সেমি  [পরিধি c=2πr=dπ সুত্রমতে]

= 28×3.1416 সেমি

= 87.9648 সেমি।

একইভাবে,

পিছনের চাকার পরিধি = 35π  সেমি = 35×3.1416 সেমি =109.956 সেমি

এখন, 88 মিটার = 88×100 সেমি = 8800 সেমি

তাহলে,

8800 সেমি পথ যেতে সামনের চাকা ঘুরবে = ⁸⁸⁰⁰/_87.9648 বার = 100 বার (প্রায়)

এবং

8800 সেমি পথ যেতে পিছনের চাকা ঘুরবে = ⁸⁸⁰⁰/_109.956 বার = 80 বার (প্রায়)

অতএব,

88 মিটার পথ যেতে সামনের চাকা পিছনের চাকা অপেক্ষা (100-80) = 20 বার বেশি ঘুরবে।

বৃত্তক্ষেত্রের ক্ষেত্রফল – ৮ম অধ্যায় ( ১৭৬ – ১৮২ পৃষ্ঠা)

 

 

বৃত্তক্ষেত্রের ক্ষেত্রফল (The Area of a Circle)

আমরা এখানে শিখন ফলাফল হিসেবে শুধুমাত্র বৃত্তক্ষেত্রের ক্ষেত্রফল এর সূত্র উল্লেখ করবো। পাঠ্যপুস্তকে বিস্তর আলোচনা করা আছে-সেখান থেকে বিস্তারিত পড়ার অনুরোধ থাকল। বৃত্তক্ষেত্রের ক্ষেত্রফল = πr² বর্গ একক যেখানে, π = 3.1416 এবং r = বৃত্তের ব্যাসার্ধ।

আবার,

বৃত্তের পরিধির সূত্রঃ 2πr একক।

একক কাজঃ

১. তোমরা প্রত্যেকে পছন্দমতো ভিন্ন ভিন্ন ব্যাসার্ধের কয়েকটি বৃত্ত আঁক। বৃত্তক্ষেত্রগুলোর ব্যাসার্ধ ব্যাস, পরিধি পরিমাপ করো। তারপর ছক কাগজ ও সূত্র দ্বারা ক্ষেত্রফল পরিমাপ করে সারণিটি পূরণ করো।

সমাধানঃ

নিজে নিজে চেষ্টা করো, আমরা এখানে একটা আনুমানিক ফলাফল তুলে ধরলাম।

বৃত্ত	ব্যাসার্ধ	ব্যাস	পরিধি সুতা বা দড়ি ব্যবহার করে)	পরিধি (সূত্র ব্যবহার করে)	ক্ষেত্রফল (ছক কাগজ ব্যবহার করে)	ক্ষেত্রফল (সূত্র ব্যবহার করে)	ছক কাগজ ও সূত্র ব্যবহার করে পাওয়া ক্ষেত্রফলদ্বয়ের মধ্যে তুলনা
১.	২ সেমি	৪ সেমি	১২.৫ সেমি	১২.৫৬৬৪ সেমি	১২.৪৪ বর্গ সেমি	১২.৫৬৬৪ বর্গ সেমি	সামান্য পার্থক্য
২.	৩ সেমি	৬ সেমি	১৮.৮ সেমি	১৮.৮৪৯৬ সেমি	২৮.২৪ বর্গ সেমি	২৮.২৭৪৪ বর্গ সেমি	সামান্য পার্থক্য
৩.	৪ সেমি	৮ সেমি	২৫.১ সেমি	২৫.১৩২৮ সেমি	৫০.২২ বর্গ সেমি	৫০.২৫৫৬ বর্গ সেমি	সামান্য পার্থক্য
৪.	৫ সেমি	১০ সেমি	৩১.৪ সেমি	৩১.৪১৬ সেমি	৭৮.৫০ বর্গ সেমি	৭৮.৫৪ বর্গ সেমি	সামান্য পার্থক্য

২. নিচের ছকটি খাতায় আঁক এবং হিসাব করে খালি ঘরগুলো পূরণ করো।

ক্রমিক নম্বর	ব্যাসার্ধ	ব্যাস	বৃত্তের পরিধি	বৃত্তের ক্ষেত্রফল
১.	১২ সেমি
২.		২১ সেমি
৩.			২৩ সেমি
৪.				২৫৪.৩৪ বর্গ সেমি

সমাধানঃ

ক্রমিক নম্বর	ব্যাসার্ধ	ব্যাস	বৃত্তের পরিধি	বৃত্তের ক্ষেত্রফল
১.	১২ সেমি	২৪ সেমি	৭৫.৩৯৮৪ সেমি	৪৫২.৩৯০৪ বর্গ সেমি
২.	১০.৫ সেমি	২১ সেমি	৬৫.৯৭৩৬ সেমি	৩৪৬.৩৬১৪ বর্গ সেমি
৩.	৩.৬৬০৫৫ সেমি	৭.৩২১১ সেমি	২৩ সেমি	৪২.০৯৬৩ বর্গ সেমি
৪.	৮.৯৯৭৭১ সেমি	১৭.৯৯৫৪১ সেমি	৫৬.৫৩৪৪ সেমি	২৫৪.৩৪ বর্গ সেমি

সমাধান সূত্রঃ

১. ব্যাস = 2r; বৃত্তের পরিধি = 2πr, বৃত্তের ক্ষেত্রফল = πr² [এখানে, ব্যাসার্ধ r = 12 সেমি, π = 3.1416]

২. ব্যাসার্ধ r = ^{ব্যাস}/₂; বৃত্তের পরিধি = 2πr, বৃত্তের ক্ষেত্রফল = πr² [এখানে, ব্যাস 2r = 21 সেমি, π = 3.1416]

৩. এখানে, পরিধি 2πr = ২৩, তাহলে, ব্যাসার্ধ r = ²³/_(2×3.1416) = 3.66 (প্রায়); ব্যাস = 2r,  বৃত্তের ক্ষেত্রফল = πr²

৪. এখানে, বৃত্তক্ষেত্রের ক্ষেত্রফল, πr² = ২৫৪.৩৪, বা, r² = ^254.34/_3.1416 = 80.9587471, বা, r = 8.99771; ব্যাস = 2r; বৃত্তের পরিধি = 2πr.

৩. পাশের চিত্রে দুইটি সমকেন্দ্রিক বৃত্ত প্রদর্শিত আছে। OAB সমকোণী ত্রিভুজটির ক্ষেত্রফল ১৮ বর্গ মিটার।

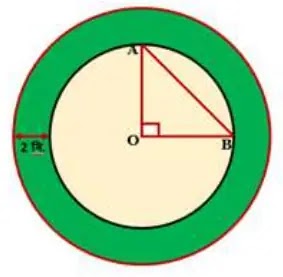
ক) ছোট বৃত্তটির পরিধি নির্ণয় করো।

খ) বড় বৃত্তটির পরিধি নির্ণয় করো।

গ) ছোট বৃত্তটির ক্ষেত্রফল নির্ণয় করো।

ঘ) বড় বৃত্তটির ক্ষেত্রফল নির্ণয় করো।

ঙ) সবুজ অংশের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

দেওয়া আছে,

OAB সমকোণী ত্রিভুজটির ক্ষেত্রফল ১৮ বর্গ মিটার।

অর্থাৎ, ½×OA×OB = 18 [যেহেতু, ত্রিভুজের ক্ষেত্রফল = ½×ভুমি×উচ্চতা]

বা, OA×OB = 18×2

বা, OA×OB = 36

বা, OB×OB = 36 [যেহেতু, O বৃত্তের কেন্দ্র এবং A ও B বৃত্তের পরিধিস্থ বিন্দু সেহেতু OA=OB=বৃত্তের ব্যাসার্ধ]

বা, OB² = 36

বা, OB = √36

বা, OB = 6

তাহলে, চিত্র অনুসারে ছোট বৃত্তের ব্যাসার্ধ r₁= 6 মিটার

এবং বড় বৃত্তের ব্যাসার্ধ r₂ = (6+2) মিটার = 8 মিটার।

(ক)

ছোট বৃত্তটির পরিধি = 2πr₁ = 2×3.1416×6 = 37.6992 মিটার।

(খ)

বড় বৃত্তটির পরিধি =  2πr₂ = 2×3.1416×8 = 50.2656 মিটার।

(গ)

ছোট বৃত্তটির ক্ষেত্রফল = πr₁² = 3.1416×6² = 113.0976 বর্গ মিটার।

(ঘ)

বড় বৃত্তটির ক্ষেত্রফল = πr₂² = 3.1416×8² = 201.0624 বর্গ মিটার।

(ঙ)

সবুজ অংশের ক্ষেত্রফল

= বড় বৃত্তটির ক্ষেত্রফল – ছোট বৃত্তটির ক্ষেত্রফল

= 201.0624 বর্গ মিটার – 113.0976 বর্গ মিটার

= 87.9648 বর্গ মিটার।

৪. একটি পুরাতন ক্যালেন্ডারের পিছনের পৃষ্ঠায় ১৫ সেন্টিমিটার ব্যাসার্ধের বৃত্ত আঁক। এবার ক্যালেন্ডারের বৃত্তাকার অংশটুকু কেটে নাও। বৃত্তাকার অংশ থেকে ২.৫ সেন্টিমিটার ব্যাসার্ধের দুইটি বৃত্তাকার অংশ এবং ৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার অংশ কেটে ফেলে দাও। বাকী অংশটুকু তোমার পছন্দমতো রং করো। তোমার রং করা অংশের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

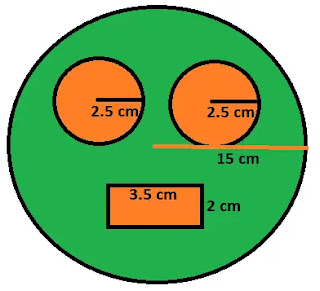
একটি ক্যালেন্ডারের পিছনের পৃষ্ঠায় ১৫ সেন্টিমিটার ব্যাসার্ধের বৃত আঁকলাম এবং ক্যালেন্ডারের বৃত্তাকার অংশটুকু কেটে নিলাম। বৃত্তাকার অংশ থেকে ২.৫ সেন্টিমিটার ব্যাসার্ধের দুইটি বৃত্তাকার অংশ এবং ৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার অংশ কেটে ফেলে দিলাম। বাকী অংশটুকু সবুজ রং করলাম। এখন সবুজ রং করা অংশের ক্ষেত্রফল নিন্মরুপে হিসাব করে বের করলাম।

১৫ সেমি ব্যাসার্ধ বিশষ্ট বৃত্তের ক্ষেত্রেফল

= π(১৫)^২ বর্গ সেমি

= ৩.১৪১৬×১৫×১৫ বর্গ সেমি 

= ৭০৬.৮৬ বর্গ সেমি

২.৫ সেমি ব্যাসার্ধ বিশষ্ট একটি বৃত্তের ক্ষেত্রেফল

= π(২.৫)^২ বর্গ সেমি

= ৩.১৪১৬×২.৫×২.৫ বর্গ সেমি

= ১৯.৬৩৫ বর্গ সেমি

২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল

= ১৯.৬৩৫×২ বর্গ সেমি

= ৩৯.২৭ বর্গ সেমি

আবার,

৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার ক্ষেত্রের ক্ষেত্রফল

= ৩.৫ সেমি × ২ সেমি

= ৭ বর্গ সেমি

এখন,

২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল ও আয়তাকার ক্ষেত্রটির ক্ষেত্রফলের সমষ্টি

= ৩৯.২৭ বর্গ সেমি + ৭ বর্গ সেমি

= ৪৬.২৭ বর্গ সেমি।

অতএব,

সবুজ অংশের ক্ষেত্রফল

= ১৫ সেমি ব্যাসার্ধ বিশষ্ট বৃত্তের ক্ষেত্রেফল – (২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল ও আয়তাকার ক্ষেত্রটির ক্ষেত্রফলের সমষ্টি)

= ৭০৬.৮৬ বর্গ সেমি – ৪৬.২৭ বর্গ সেমি

= ৬৬০.৫৯ বর্গ সেমি (Ans.)

৫. একটি বৃত্তাকার পার্কের ব্যাস ২৫ মিটার। পার্কটিকে বেষ্টন করে ভিতরে ২ মিটার প্রশস্ত একটি পথ আছে। পথটির ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

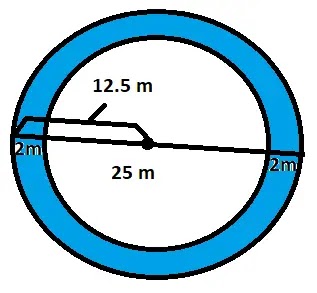
বৃত্তাকার পার্কের ব্যাস = ২৫ মিটার।

তাহলে, বৃত্তাকার পার্কের ব্যাসার্ধ = ^২৫/_২ মিটার = ১২.৫ মিটার।

অতএব,

বৃত্তাকার পার্কের ক্ষেত্রফল

= π(১২.৫)^২ বর্গ মিটার

= ৩.১৪১৬×১২.৫×১২.৫ বর্গ মিটার

= ৪৯০.৮৭৫ বর্গ মিটার।

এখন,

পথ বাদে বৃত্তাকার পার্কের ব্যাসার্ধ = (১২.৫-২) মিটার = ১০.৫ মিটার।

তাহলে,

পথ বাদে বৃত্তাকার পার্কের ক্ষেত্রফল

= π(১০.৫)^২ বর্গ মিটার

= ৩.১৪১৬×১০.৫×১০.৫ বর্গ মিটার

= ৩৪৬.৩৬১৪ বর্গ মিটার

সুতরাং,

পথটির ক্ষেত্রফল

= বৃত্তাকার পার্কের ক্ষেত্রফল – পথ বাদে বৃত্তাকার পার্কের ক্ষেত্রফল

= ৪৯০.৮৭৫ বর্গ মিটার – ৩৪৬.৩৬১৪ বর্গ মিটার

= ১৪৪.৫১৩৬ বর্গ মিটার।

৬. কাগজ কেটে পাশের চিত্রের মতো ৬ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট একটি বৃত্তক্ষেত্র কেটে নাও। এবার ৫ সেন্টিমিটার ব্যাস বিশিষ্ট আরো চারটি বৃত্তক্ষেত্র কেটে নাও।

এবার ছোট বৃত্তক্ষেত্রগুলো তোমার পছন্দমতো রং করে উপরের চিত্রের মতো বড় বৃত্তের ভিতরে আঁঠা দিয়ে বসাও। এখন নিচের ছকটি খাতায় তৈরি করে ফাঁকা ঘরগুলো পূরণ করো।

ক্রমিক নং	বৃত্তের ব্যাসার্ধ	ব্যাস	পরিধি	ক্ষেত্রফল
১.	৬ সেমি
২.		৫ সেমি
৩.	বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল

সমাধানঃ

ক্রমিক নং	বৃত্তের ব্যাসার্ধ	ব্যাস	পরিধি	ক্ষেত্রফল
১.	৬ সেমি	১২ সেমি	৩৭.৬৯৯২ সেমি	১১৩.০৯৭৬ বর্গ সেমি
২.	২.৫ সেমি	৫ সেমি	১৫.৭০৮ সেমি	১৯.৬৩৫ বর্গ সেমি
৩.	বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল			{১১৩.০৯৭৬ – (১৯.৬৩৫×৪)} = ৩৪.৫৫৭৬ বর্গ সেমি

ব্যাখ্যাঃ

৬ সেমি ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল = π(৬)^২ বর্গ সেমি = ১১৩.০৯৭৬ বর্গ সেমি

২.৫ ব্যাসার্ধ বশিষ্ট ১টি বৃত্তের ক্ষেত্রফল = π(২.৫)^২ বর্গ সেমি = ১৯.৬৩৫ বর্গ সেমি

২.৫ ব্যাসার্ধ বশিষ্ট ৪টি বৃত্তের ক্ষেত্রফল = (৪×১৯.৬৩৫) বর্গ সেমি = ৭৮.৫৪ বর্গ সেমি

তাহলে,

বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল

= ৬ সেমি ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল – ২.৫ ব্যাসার্ধ বশিষ্ট ৪টি বৃত্তের ক্ষেত্রফল

= ১১৩.০৯৭৬ বর্গ সেমি – ৭৮.৫৪ বর্গ সেমি

= ৩৪.৫৫৭৬ বর্গ সেমি।

৭. ফাতিন তার বড় বোন লামিয়ার সাথে পিজ্জা হাটে গেল পিজ্জা কিনবে বলে। দোকানে ঝুলিয়ে রাখা মূল্য তালিকায় দুই ধরনের প্যাকেজ দেখতে পেলো। উভয় প্যাকেজের পিজ্জার উচ্চতা সমান।

ক. ৩৫ সেন্টিমিটার ব্যাস বিশিষ্ট একজোড়া পিজ্জার দাম ৩০০ টাকা

খ. ৩০ সেন্টিমিটার ব্যাস বিশিষ্ট তিনটি পিজ্জার দাম ৩৫০ টাকা

কোন প্যাকেজটি কিনলে ফাতিন ও লামিয়া লাভবান হবে?

সমাধানঃ

৩৫ সেমি ব্যাস বিশিষ্ট ১টি পিজ্জার ক্ষেত্রফল

= π(^৩৫/_২)^২ বর্গ সেমি  [যেহেতু, ব্যাসার্ধ =^৩৫/_২]

= ৯৬২.১১৫ বর্গ সেমি

তাহলে,

৩৫ সেমি ব্যাস বিশিষ্ট ২টি পিজ্জার ক্ষেত্রফল

= (৯৬২.১১৫×২) বর্গ সেমি

= ১৯২৪.২৩ বর্গ সেমি

এখন,

১৯২৪.২৩ বর্গ সেমি পিজ্জার দাম ৩০০ টাকা

∴ ১ বর্গ সেমি পিজ্জার দাম = ^৩০০/_{১৯২৪.২৩} টাকা = ০.১৫৫৯১ টাকা (প্রায়)……(i)

আবার,

৩০ সেন্টিমিটার ব্যাস বিশিষ্ট ১টি পিজ্জার ক্ষেত্রফল

= π(^৩০/_২)^২ বর্গ সেমি  [যেহেতু, ব্যাসার্ধ =^৩০/_২]

= ৭০৬.৮৬ বর্গ সেমি

তাহলে,

৩০ সেন্টিমিটার ব্যাস বিশিষ্ট ৩টি পিজ্জার ক্ষেত্রফল

= (৭০৬.৮৬×৩) বর্গ সেমি

= ২১২০.৫৬ বর্গ সেমি

এখন,

২১২০.৫৬ বর্গ সেমি পিজ্জার দাম ৩৫০ টাকা

∴ ১ বর্গ সেমি পিজ্জার দাম = ^৩৫০/_{২১২০.৫৬} টাকা = ০.১৬৫০৫১ টাকা (প্রায়)……(ii)

এখন, (i) ও (ii) সমীকরণ হতে দেখতে পাই, ১ বর্গ সেমি পিজ্জার দামের ক্ষেত্রে ৩৫ সেমি ব্যাস বিশিষ্ট পিজ্জার দাম কম তুলনামূলক কম। [যেহেতু, ০.১৫৫৯১ < ০.১৬৫০৫১]

অতএব,

ক প্যাকেজটি কিনলে ফাতিন ও লামিয়া লাভবান হবে।

৮. বৃত্তাকার সামগ্রী প্রদর্শন ও খটিুঁ নাটি হিসাব সংক্রান্ত প্রজেক্টঃ শ্রেণির সকল শিক্ষার্থীরা কয়েকটি দলে বিভক্ত হয়ে দৈনন্দিন জীবনে ব্যবহৃত ও পরিচিত বৃত্তাকার জিনিসপত্র সংগ্রহ করে জিনিসপত্রগুলোর ব্যাসার্ধ ব্যাস, পরিধি ও ক্ষেত্রফল মেপে হিসাবসহ প্রদর্শন করো। দলের সকল সদস্য পরস্পরের সাথে আলোচনা করে অন্যান্য দলের সামনে উপস্থাপন করো।

সমাধানঃ

নিজেরা করো।

৯. রুমাল, নেপকিন, কুশন বা যেকোনো কাপড়ে বিভিন্ন রকমের সূতা দিয়ে নকশা তৈরি করা নীতুর পছন্দের একটি কাজ। লেখাপড়ার পাশাপাশি অবসর সময়ে সে কাপড়ের উপর সুই-সূতা দিয়ে বিভিন্ন রকমের নকশা তৈরি করে। নীতু যে বৃত্তাকার চাকতিটি (Embroydery Hoop) ব্যবহার করে তার ব্যাসার্ধ ১৫ সেন্টিমিটার।

ক) চাকতিটির পরিধি নির্ণয় করো।

খ) চাকতির ভিতরের কাপড়ের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

(ক)

চাকতির ব্যাসার্ধ r = ১৫ সেমি

অতএব,

চাকতিটির পরিধি

= ২πr সেমি

= ২×৩.১৪১৬×১৫ সেমি

= ৯৪.২৪৮ সেমি।

(খ)

চাকতির ভিতরের কাপড়ের ক্ষেত্রফল

= πr^২ বর্গ সেমি

= ৩.১৪১৬×(১৫)^২ বর্গ সেমি

= ৩.১৪১৬×১৫×১৫ বর্গ সেমি

= ৭০৬.৮৬ বর্গ সেমি।

পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

👉 অজানা রাশির উৎপাদক – ৯ম অধ্যায়(১ম অংশ) – সমাধান | গণিত | সপ্তম শ্রেণী | Class 7 Math Chapter 9 | BD 2023