
এই পোস্টে আমরা জানব ষষ্ঠ শ্রেনীর, বিষয় গণিত এর নবম অধ্যায়, সরল সমীকরণ সম্পর্কে।
x+2=5 হলো একটি গাণিতিক বাক্য ও সমতা। আর সমান চিহ্ন সংবলিত এই প্রকার গাণিতিক বাক্যকে আমরা সমীকরণ বলে থাকি। এখানে অজানা বা অজ্ঞাত রাশি কে চলক (variable) বলি। সাধারণত ইংরেজি বর্ণমালার বর্ণ ছোট হাতের অক্ষরগুলোকে অজ্ঞাত রাশি বা চলক হিসেবে ব্যবহার করা হয়। অজ্ঞাত রাশি বা চলকের একঘাতবিশিষ্ট সমীকরণই হলো সরল সমীকরণ বা Linear Equation। যেমন: 2a-5=0, y+3 =11, 2a-1=a+5 ইত্যাদি। কেননা এদের প্রত্যেকটি এক চলকবিশিষ্ট ও একঘাতবিশিষ্ট। এখন চল আমরা অনুশীলনীর সমস্যার সমাধান করিঃ-
ষষ্ঠ শ্রেণি নবম অনুশীলনী
১। ছক তৈরি করে নিচের কোনগুলো সমীকরণ এবং কোনগুলো সমীকরণ নয় যুক্তিসহ উপস্থাপন করো।
(a) 15 = x + 5
(b) (y-6) < 3
(c) 6/3 = 2
(d) z – 4 = 0
(e) (4×3) – 12 = 0
(f) 2x + 3 = x – 15
(g) y + 25 > 30
(h) 8 – x = 11
(i) 20 – (10-5) = 3×5
(j) 5/0 = 5
(k) 15y = 45
(l) 7 = (11×2) + x
সমাধানঃ
| ক্রমিক নম্বর | বীজগাণিতিক সম্পর্ক | সমীকরণপরীক্ষার ফল | ফলাফলের কারন ব্যাখ্যা |
| (a) | 15 = x + 5 | সমীকরণ | এখানে, চলক x বিদ্যমান এবং x এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
| (b) | (y-6) < 3 | সমীকরণ নয় | এখানে, চলক y থাকলেও y এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান হবে না। |
| (c) | 6/3 = 2 | সমীকরণ নয় | এখানে, কোন চলকই নেই। |
| (d) | z – 4 = 0 | সমীকরণ | এখানে, চলক z বিদ্যমান এবং z এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
| (e) | (4×3) – 12 = 0 | সমীকরণ নয় | এখানে, কোন চলকই নেই। |
| (f) | 2x + 3 = x – 15 | সমীকরণ | এখানে, চলক x বিদ্যমান এবং x এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
| (g) | y + 25 > 30 | সমীকরণ নয় | এখানে, চলক y থাকলেও y এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান হবে না। |
| (h) | 8 – x = 11 | সমীকরণ | এখানে, চলক x বিদ্যমান এবং x এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
| (i) | 20 – (10-5) = 3×5 | সমীকরণ নয় | এখানে, কোন চলকই নেই। |
| (j) | 5/0 = 5 | সমীকরণ নয় | এখানে, কোন চলকই নেই। |
| (k) | 15y = 45 | সমীকরণ | এখানে, চলক y বিদ্যমান এবং y এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
| (l) | 7 = (11×2) + x | সমীকরণ | এখানে, চলক x বিদ্যমান এবং x এর নির্দিষ্ট মানের জন্য বামপক্ষ ও ডানপক্ষ সমান। |
২। নিচের ছকের সমস্যাগুলোকে সমীকরণ আকারে প্রকাশ করা হলো।
সমাধান :
| ক্রমিকনম্বর | সমস্যা | সমীকরণ | সমীকরণের মূল |
| (i) | একটি সংখ্যা x এর দ্বিগুণের সাথে 7 যোগ করলে যোগফল 23 হবে। | 2x + 7 = 23 | 2x + 7 = 23 বা, 2x = 23 – 7 বা, 2x = 16 বা, x =16/2 বা, x =8 অতএব, সমীকরনের মূল = 8 |
| (ii) | দুইটি ক্রমিক স্বাভাবিক বিজোড় সংখ্যার যোগফল 36 এবং ছোট সংখ্যাট y | y + (y + 2) =36 | y + (y + 2) = 36 বা, 2y + 2 = 36 বা, 2y = 34 বা, y = 17 অতএব, সমীকরনের মূল = 17 |
| (iii) | একটি সংখ্যা x এর চার গুণ থেকে 5 বিয়োগ করলে প্রাপ্ত বিয়োগফল সংখ্যাটির দ্বিগুণ অপেক্ষা 19 বেশি। | 4x – 5 = 2x +19 | 4x – 5 = 2x + 19 বা, 4x – 2x = 19 + 5 বা, 2x = 24 বা, x = 12 অতএব, সমীকরনের মূল = 12 |
| (iv) | একটি আয়তাকার পুকুরের দৈর্ঘ্য x মিটার, দৈর্ঘ্য অপেক্ষা প্রস্থ 3 মিটার কম এবং পুকুরটির পরিসীমা 26 মিটার। | 2{x + (x-3)} = 26 | 2{x + (x-3)} = 26 বা, 2(2x-3) = 26 বা, 2x – 3 = 13 বা, 2x = 16 বা, x = 8 অতএব, সমীকরনের মূল = 8 |
| (v) | পুত্রের বর্তমান বয়স y বছর, পিতার বয়স পুত্রের বয়সের ছয় গুণ। তাদের বর্তমান বয়সের সমষ্টি 35 বছর। | y + 6y = 35 | y + 6y = 35 বা, 7y = 35 বা, y = 5 অতএব, সমীকরনের মূল = 5 |
৩। প্রতিটি সমীকরণের পাশে থাকা কলামের ভিতরের মানগুলো থেকে সঠিক মূলটি বেছে নাও। অবশিষ্ট মানগুলো কেন সমীকরণটির মূল হবে না ব্যাখ্যা করো।
| ক্রমিক নম্বর | সমীকরণ | মান |
| (i) | 2x+5=15 | 10,5,-5 |
| (ii) | 5-y=7 | 12,2,-2 |
| (iii) | 5x-2=3x+8 | 5,1,-5 |
| (iv) | 2y+2=16 | 18,9,7 |
| (v) | 4z-5=2z+19 | 12,7,4 |
সমাধানঃ
(i)
2x+5=15
বা, 2x=15-5
বা, 2x=10
বা, x=10/2
বা, x=5
অতএব, সঠিক মূল 5
এখন, x=10 হলে, বামপক্ষ = 2.10+5 = 20+5 =25 যা ডানপক্ষের সমান নয়।
আবার, x=-5 হলে, বামপক্ষ = 2.(-5)+5 = -10+5 =-5 যা ডানপক্ষের সমান নয়।
এই কারনে, 10 ও -5, 2x+5=15 এর মূল হবে না।
(ii)
5-y=7
বা,-y = 7-5
বা, -y = 2
বা, y = -2
অতএব, সঠিক মূল -2
এখন,
y=12 হলে, বামপক্ষ = 5-12 = -7 যা ডানপক্ষের সমান নয়।
আবার। y=2 হলে, বামপক্ষ = 5-2 = 3 যা ডানপক্ষের সমান নয়।
এই কারনে, 12 ও 2, 5-y=7 এর মূল হবে না।
(iii)
5x-2=3x+8
বা, 5x-3x = 8 + 2
বা, 2x = 10
বা, x = 5
অতএব, সঠিক মূল 5
এখন,
x=1 হলে, বামপক্ষ = 5.1-2 =5-2 =3; ডানপক্ষ = 3.1+8 = 3+8 =11; অর্থাৎ দুই পক্ষ সমান নয়।
আবার,
x=-5 হলে, বামপক্ষ = 5.(-5)-2 =-25-2 =-27; ডানপক্ষ = 3.(-5)+8 = -15+8 =-7; অর্থাৎ দুই পক্ষ সমান নয়।
এই কারনে, 1 ও -5, 5x-2=3x+8 এর মূল হবে না।
(iv)
2y+2=16
বা, 2y = 16-2
বা, 2y = 14
বা, y = 14/2
বা, y = 7
অতএব, সঠিক মূল 7
এখন, x=18 হলে, বামপক্ষ = 2.18+2 = 36+2 =38 যা ডানপক্ষের সমান নয়।
আবার, x=9 হলে, বামপক্ষ = 2.9+2 = 18+2 =20 যা ডানপক্ষের সমান নয়।
এই কারনে, 18 ও 9, 2y+2=16 এর মূল হবে না।
(v)
4z-5=2z+19
বা, 4z-2z=19+5
বা, 2z=24
বা, z=24/2
বা, z=12
অতএব, সঠিক মূল 12
এখন,
z=7 হলে, বামপক্ষ = 4.7–5=28-5=23; ডানপক্ষ = 2.7+19=14+19=33; অর্থাৎ দুই পক্ষ সমান নয়।
আবার,
z=4 হলে, বামপক্ষ = 4.4-5=16-5=11; ডানপক্ষ = 2.4+19=8+19=27; অর্থাৎ দুই পক্ষ সমান নয়।
এই কারনে, 7 ও 4, 4z-5=2z+19 এর মূল হবে না।
👉 ত্রিমাত্রিক বস্তুর গল্প – সমাধান | গণিত – ১০ম অধ্যায় | ষষ্ঠ শ্রেণী
8। মীনা 100 টাকার একটি নোট নিয়ে বাজারে গেল। সে একটি দোকান থেকে প্রতিটি x টাকা দামের এক ডজন কলম কিনল। দোকানদার তাকে 40 টাকা ফেরত দিলেন। মীনা অন্য একটি দোকান থেকে প্রতিটি 12 টাকা দামের yটি খাতা কেনায় 4 টাকা অবশিষ্ট রইল।
ক) প্রতিটি কলমের মূল্য নির্ণয় করো।
খ) মীনা কয়টি খাতা কিনেছিল?
সমাধানঃ
(ক)
এক ডজন = 12 টি
একটি কলমের দাম x টাকা
∵12 টি কলমের দাম 12x টাকা
প্রশ্নমতে,
100 – 12x = 40
বা, -12x = 40 -100
বা, 12x = 100-40
বা, 12x =60
বা, x = 60/12
বা, x = 5
অতএব, প্রতিটি কলমের মূল্য 5 টাকা।
(খ)
1 টি খাতার দাম 12 টাকা
∵ y টি খাতার দাম 12y টাকা।
প্রশ্নমতে,
40 – 12y = 4
বা, -12y = 4 -40
বা, 12y = 40-4
বা, 12y =36
বা, y =36/12
বা, y = 3
অতএব, মিনা খাতা কিনেছিল 3 টি।
৫। করিম সাহেব তাঁর 56000 টাকার কিছু টাকা বার্ষিক 12% মুনাফায় ও বাকি টাকা বার্ষিক 10% মুনাফায় বিনিয়োগ করলেন। এক বছর পর তিনি মোট 6400 টাকা মুনাফা পেলেন। তিনি 10% মুনাফায় কত টাকা বিনিয়োগ করেছেন?
সমাধানঃ
মনে করি, করিম সাহেব 10% মুনাফায় বিনিয়োগ করেছেন x টাকা
তাহলে, করিম সাহেব 12% মুনাফায় বিনিয়োগ করেছেন (56000-x) টাকা
প্রশ্নমতে,
(56000-x)×12% + x×10% = 6400
বা, (56000-x)×12/100 + x×10/100 = 6400
বা, (56000-x)×12 + x×10 = 6400×100 [উভয়পক্ষকে 100 দ্বারা গুণ করে]
বা, 56000×12-12x+10x = 640000
বা, 672000 – 2x = 640000
বা, -2x = 640000 – 672000
বা, 2x = 672000 – 640000
বা, 2x = 32000
বা, x = 32000/2
বা, x = 16000
অতএব, তিনি 10% মুনাফায় 16000 টাকা বিনিয়োগ করেছেন।
👉 অজানা রাশির জগৎ – সমাধান | গণিত – ৮ম অধ্যায় | ষষ্ঠ শ্রেণী
৬। কোনো এক ক্রিকেট ম্যাচে সাকিব, মুশফিকুর রহিমের দ্বিগুণ রান করে। মাত্র 2 রানের জন্য দুজনের রানের সমষ্টি ডাবল সেঞ্চুরি হয় নাই। কে কত রান করেছে?
সমাধানঃ
আমরা জানি ক্রিকেটে সেঞ্চুরি হয় 100 রান করলে
আর ডাবল-সেঞ্চুরি হয় 200 রান করলে।
তাহলে, ম্যাচটিতে সাকিব ও মুশফিকের রানের সমষ্টি (200-2) = 198 রান।
এখন মনে করি,
মুশফিক ম্যাচটিতে যত রান করে তার সংখ্যা = x
সুতরাং ম্যাচটিতে সাকিব যত রান করে তার সংখ্যা = 2x
প্রশ্নমতে,
x + 2x = 198
3x = 198
x = 198/3
x = 66
অর্থাৎ, মুশফিক ম্যাচটিতে 66 রান করেছে।
এবং সাকিব ম্যাচটিতে (66×2) = 132 রান করেছে।
৭। খালি ঘর পূরণ করো।
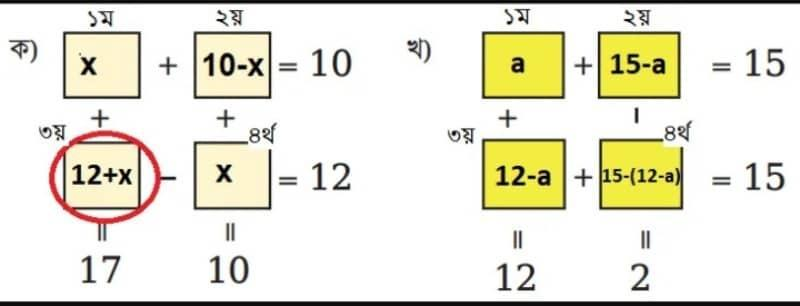
সমাধানঃ
(ক)
মনে করি ১ম খালি ঘর = x
এখন,
১ম খালি ঘর + ২য় খালি ঘর = 10
বা, x + ২য় খালি ঘর = 10
বা, ২য় খালি ঘর = 10-x
আবার,
২য় খালি ঘর + ৪র্থ খাকি ঘর = 10
বা, 10-x + ৪র্থ খাকি ঘর = 10
বা, ৪র্থ খাকি ঘর = 10 – (10 -x) = 10 – 10 + x = x
বা, ৪র্থ খালি ঘর = x
আবার,
৩য় খালিঘর – ৪র্থ খালিঘর = 12
বা, ৩য় খালি ঘর – x =12
বা, ৩য় খালিঘর = 12+x
এখন,
১ম খালি ঘর + ৩য় খালি ঘর = 17
বা, x + 12+x = 17
বা, 2x = 17-12
বা, 2x = 5
বা, x = 2.5
তাহলে,
১ম খালি ঘর = 2.5
২য় খালি ঘর = 10-2.5 = 7.5
৩য় খালি ঘর = 2.5
৪র্থ খালি ঘর = 12+2.5 =14.5
প্রিয় শিক্ষার্থী, তোমরা এই মানগুলো চিত্রে প্রদত্ত স্থানে বসাবে, এখানে আমরা শুধু কিভাবে খালি ঘরের মান বের করা যায় সেটা দেখালাম। ধন্যবাদ।
(খ)
ধরি, ১ম খালি ঘরের মান = a
এখন,
১ম খালি ঘর + ২য় খালি ঘর = 15
বা, a + ২য় খালি ঘর = 15
বা, ২য় খালি ঘর = 15-a
আবার,
১ম খালিঘর + ৩য় খালিঘর = 12
বা, a + ৩য় খালিঘর = 12
বা, ৩য় খালি ঘর = 12-a
আবার,
৩য় খালি ঘর + ৪র্থ খালি ঘর = 15
বা, 12-a + ৪র্থ খালি ঘর = 15
বা, ৪র্থ খালি ঘর = 15 – (12-a) = 15 – 12 + a = 3+a
এখন,
২য় খালি ঘর – ৪র্থ খালি ঘর = 2
বা, (15-a) – (3+a) = 2
বা, 15 – a – 3 – a = 2
বা, 12 – 2a = 2
বা, -2a = 2-12
বা, -2a = -10
বা, 2a = 10
বা, a = 10/2 = 5
তাহলে,
১ম খালি ঘর = a = 5
২য় খালি ঘর = 15-a = 15-5 = 10
৩য় খালি ঘর = 12-a = 12-5 = 7
৪র্থ খালি ঘর = 3+a= 3+5 = 8
প্রিয় শিক্ষার্থী, তোমরা এই মানগুলো চিত্রে প্রদত্ত স্থানে বসাবে, এখানে আমরা শুধু কিভাবে খালি ঘরের মান বের করা যায় সেটা দেখালাম। ধন্যবাদ।
৮। পানির একটা বোতলের ওজন 150 গ্রাম। মিনা 50 গ্রাম ওজনের একটা ব্যাগের মধ্যে কিছু সংখ্যক পানির বোতল রাখল। বোতলের সংখ্যাকে x দ্বারা এবং পানির বোতলগুলোর ওজন ও ব্যাগের ওজনের যোগফল y দ্বারা প্রকাশ করা হলো।
ক) x এবং y এর সম্পর্ক সমীকরণের মাধ্যমে লেখো।
খ) y এর মান নির্ণয় করো যখন x = 15
গ) x এর মান নির্ণয় করো যখন y = 1100
সমাধানঃ
দেওয়া আছে,
বোতলের সংখ্যা = x
1 টি বোতলের ওজন 150 গ্রাম
ব্যাগের ওজন = 50 গ্রাম
পানির বোতলগুলোর ওজন + ব্যাগের ওজন = y
(ক)
1 টি বোতলের ওজন 150 গ্রাম
∵ x টি বোতলের ওজন = 150x গ্রাম
তাহলে, বোতলগুলোর ওজন + ব্যাগের ওজন = y
বা, 150x + 50 = y
∵ x এবং y এর সম্পর্ক সমীকরণ: 150x + 50 = y
(খ)
ক হতে পাই,
150x + 50 = y
বা, y = 150x + 50
বা, y = 150×15 + 50 [প্রশ্নমতে, x=15]
বা, y = 2300
(গ)
ক হতে পাই,
150x + 50 = y
বা, 150x + 50 = 1100 [প্রশ্নমতে, y = 1100]
বা, 150x = 1100 – 50
বা, 150x = 1050
বা, x = 1050/150
বা, x = 7
৯। x প্যাকেট বিস্কুট এবং এক বোতল পানীয়ের মূল্য একত্রে y টাকা । এক প্যাকেট বিস্কুটের মূল্য 20 টাকা এবং এক বোতল পানীয়ের মূল্য 15 টাকা।
ক) x এবং y এর সম্পর্ক সমীকরণের মাধ্যমে লেখো
খ) y এর মান নির্ণয় কর যখন x = 25
গ) x এর মান নির্ণয় কর যখন y = 255
সমাধানঃ
(ক)
এক প্যাকেট বিস্কুটের মূল্য 20 টাকা
∵ x প্যাকেট বিস্কুটের মূল্য 20x টাকা
এখন,
X প্যাকেট বিস্কুটের মূল্য + এক বোতল পানীয়ের মূল্য = y
বা, 20x + 15 = y
∵ x এবং y এর সম্পর্ক সমীকরণ: 20x + 15 = y
(খ)
ক হতে পাই,
20x + 15 = y
বা, 20×25 + 15 = y [মান বসিয়ে, যখন x=25]
বা, 500 + 15 = y
বা, y = 515
(গ)
ক হতে পাই,
20x + 15 = y
বা, 20x + 15 = 255 [মান বসিয়ে, যখন y=255]
বা, 20x = 255 – 15
বা, 20x = 240
বা, x = 240/20
বা, x = 12
১০। তোমার শিক্ষা প্রতিষ্ঠানের খেলার মাঠটির দৈর্ঘ্য, প্রস্থ অপেক্ষা 16 মিটার বেশি।
ক) খেলার মাঠটির প্রস্থ x মিটার হলে, মাঠটির পরিসীমা x এর মাধ্যমে নির্ণয় করো।
খ) মাঠটির পরিসীমা 120 মিটার হলে, মাঠের ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
(ক)
দেওয়া আছে,
খেলার মাঠটির প্রস্থ x মিটার
∵ খেলার মাঠটির দৈর্ঘ্য = x+16 মিটার
তাহলে,
খেলার মাঠটির পরিসীমা
= 2×(দৈর্ঘ্য+প্রস্থ) একক
= 2×{(x+16)+x} মিটার
= 2×(x+16+x) মিটার
= 2(2x+16) মিটার
= 4x + 32 মিটার
∵ x এর মাধ্যমে নির্নিত মাঠটির পরিসীমাঃ 4x + 32 মিটার।
(খ)
দেওয়া আছে, মাঠটির পরিসীমা = 120 মিটার।
এখন,
ক হতে পাই,
মাঠটির পরিসীমা = 4x + 32
তাহলে,
4x + 32 = 120
বা, 4x = 120 – 32
বা, 4x = 88
বা, x = 88/4
বা, x = 22
অর্থাৎ, মাঠটির প্রস্থ = 22 মিটার
∵ মাঠটির দৈর্ঘ্য = (22 + 16) মিটার = 38 মিটার.
তাহলে,
মাঠের ক্ষেত্রফল
= দৈর্ঘ্য×প্রস্থ বর্গ একক
= 38×22 বর্গ মিটার
= 836 বর্গ মিটার।

