
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর পঞ্চম অধ্যায় আকৃতি দিয়ে যায় চেনা, সম্পর্কে।
আকৃতি দিয়ে যায় চেনা
মনে করো, তোমরা নতুন বাসায় গিয়ে উঠেছো। সেখানে তোমাকে নতুন ঘর দেওয়া হয়েছে। ঘরে বিছানা, আলমারি, ড্রয়ার, বেডসাইড টেবিল সবই আছে। এক পাশের দেয়াল জুড়ে বিশাল জানালাও আছে, সেখান দিয়ে চমৎকার আলো আসে। কিন্তু তোমার প্রিয় পড়ার টেবিল আর চেয়ারটা নাই। এত সুন্দর একটা ঘর পেলে কিন্তু পড়ার জায়গা পাওয়া যাচ্ছে না, কি বিপদ না? নিচের ছবিতে দেখো, সবকিছুর মাপ কত ফিট করে বলে দেওয়া আছে। তোমার বড় শখ পড়ার টেবিলটিতে জানালা দিয়ে আলো এসে পড়বে। এর মাঝে আবার আলমারিটি দেয়াল থেকে সরানো যায় না। আর ঘর থেকে কিছু জিনিস সরিয়ে বাইরে রাখবে তারও উপায় নাই, তবে কিছু আসবাবের স্থান পরিবর্তন করতে পারবে। এখন কী করে টেবিল আর চেয়ারটি একটি পছন্দমত জায়গায় বসাতে পারবে? একটু আভাস দিই, তুমি ঠিক ঠিক মাপে কাগজ কেটে এই সমস্যার সমাধান করার চেষ্টা করতে পারো।
সমাধানঃ
আমি নিচের চিত্র অনুরুপ সমস্যাটির সমাধান করলামঃ
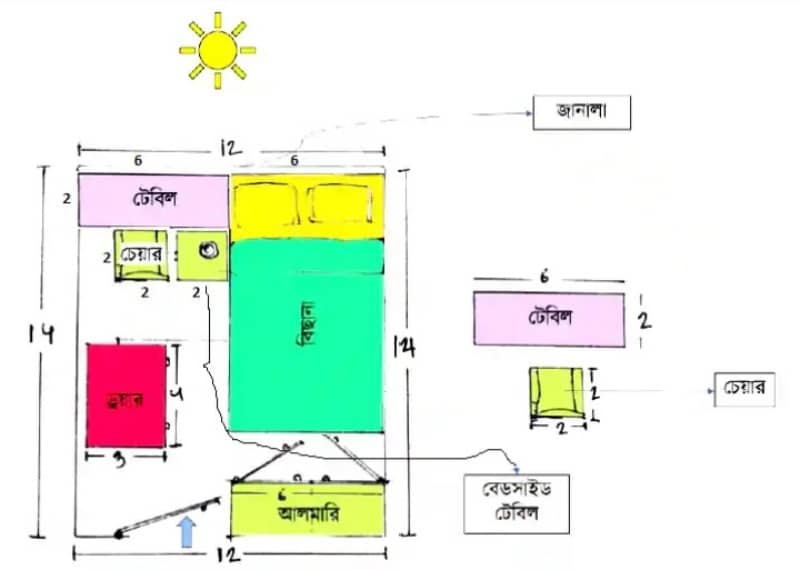
শিখনঃ আকৃতি দিয়ে যায় চেনা এর এই সমস্যা হতে আমরা বিভিন্ন বস্তুর আকৃতি সম্পর্কে বুঝতে পারলাম যখন বস্তুগুলিকে ঘরে সাজাতে গিয়ে দেখলাম এরা কতটুকু জায়গা দখল করে বা এদের পরিমাম কত সেটা বিবেচনা করে।
কাজ ১-৭ঃ
প্রতিটি কাজ পাঠ্যপুস্তকে সুন্দরভাবে বর্ণনা করা আছে। শিক্ষার্থীরা সেগুলো সুন্দরভাবে পড়ে এবং নিজে ও শিক্ষকের সহায়তায় সম্পপূর্ণ করবে।
দলগত কাজঃ
৪-৫ জনের দলে ভাগ হয়ে কোণের সমদ্বিখণ্ডক এবং রেখাংশের সমদ্বিখণ্ডকের মাঝে একটি মিল এবং একটি পার্থক্য বের করো।
সমাধানঃ
কোণের সমদ্বিখন্ডক এবং রেখাংশের সমদ্বিখন্ডক এর মধ্যকার মিল এবং অমিল (পার্থক্য) নিন্মরুপঃ
[উল্লেক্ষ্যঃ আমরা এখানে একাধিক মিল ও পার্থক্য উল্লেখ করলাম।]
| মিল | অমিল (পার্থক্য) |
| ১. উভয় সমদ্বিখন্ডক উভয়কেই সমান দুই ভাগে ভাগ করে। | ১. কোণের সমদ্বিখন্ডক কোণকে সমদ্বিখন্ডিত করে কিন্তু রেখাংশের সমদ্বিখন্ডক রেখাংশকে সমদ্বিখন্ডিত করে। |
| ২. উভয় সমদ্বিখন্ডকই কোণ উৎপন্ন করে। | ২. রেখাংশের সমদ্বিখন্ডক রেখাংশকে সমকোণে বিভক্ত করে কিন্তু কোণের সমদ্বিখন্ডক কোণকে সমকোণে বিভক্ত করতেও পারে আবার নাও পারে। |
কাজ ৮ঃ পাঠ্যপুস্তক দেখ।
দলগত কাজ: চার/পাঁচজন করে একটি দল গঠন করো এবং প্রত্যেক দল একটি করে কাগজ নাও। এবারে নিচের ধাপগুলো অনুসরণ করো।
সমাধানঃ পাঠ্যপুস্তক অনুসরন করো।
কিছু গুরুত্বপূর্ণ শিখন ফলাফলঃ
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে একান্তর কোণেরা পরস্পর সমান হয়।
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে ছেদকের একই পাশের অন্তঃস্থ কোণের পরিমাপের যোগফল দুই সমকোণের সমান হয়।
সামান্তরিকের বিপরীত কোণগুলি সমান।
একক কাজঃ
১। তোমার ইচ্ছামতো কাগজ কেটে একটি সামান্তরিক তৈরি করো।
এরপর নিচের কাজগুলি করোঃ
ক) সামান্তরিকটিকে নিচের ছবির মতো করে কেটে দুই টুকরা করে কোণ গুলিকে মিলিয়ে দেখো।
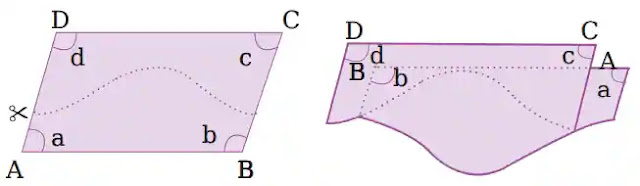
খ) সামান্তরিকটিকে নিচের ছবির মতো করে কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে দেখো।
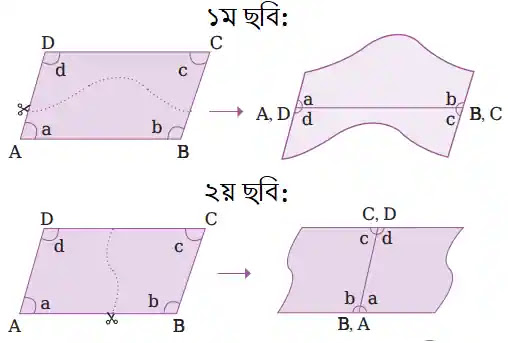
সমাধানঃ
আমার ইচ্ছামত কাগজ কেটে নিচের চিত্রের মত একটি সামন্তরিক তৈরি করলাম।
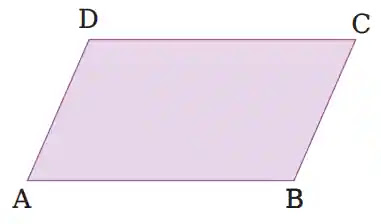
(ক)
সামন্তরিকটিকে ‘ক’ এ প্রদত্ত চিত্রের মতো করে কেটে দুই টুকরা করে কোণগুলিকে মিলিয়ে দেখলাম। ফলাফল হিসেবে পেলামঃ
∠a = ∠c
∠b = ∠d
অর্থাৎ, এর থেকে আমরা সিদ্ধান্তে বলতে পারি যে, সামন্তরিকের বিপরীত কোণগুলি পরস্পর সমান।
(খ)
সামন্তরিকটিকে প্রদত্ত ১ম ছবির মত কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে পেলামঃ
a+d = 180°
b+c = 180°
আবার,
সামন্তরিকটিকে খ এ প্রদত্ত ২য় ছবির মত কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে পেলামঃ
∠a+∠b = 180°
∠b+∠d = 180°
অর্থাৎ, এর থেকে আমরা সিদ্ধান্তে বলতে পারি যে, সামন্তরিকের সন্নিহিত দুইটি কোণের সমষ্টি 180°.
নিচের সমস্যাগুলো কাঠি দিয়ে অথবা কাগজ ভাঁজ করে সমাধান করো।
২।
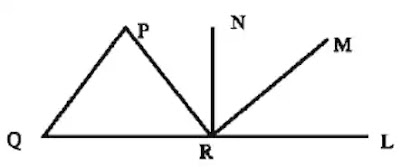
চিত্রে কোণ PQR=55° , কোণ LRN=90° এবং PQ ও MR পরস্পর সমান্তরাল। তাহলে কোণ MRN এর মান কত?
সমাধানঃ
প্রথমে দুইটি কাঠি PQ ও RM নিই এবং তাদেরকে সমান্তরালে স্থাপন করি। এখন আরও একটি কাঠি QL নিই এবং এটিকে এমন ভাবে স্থাপন করি যাতে PQ ও RM যথাক্রমে Q ও R বিন্দুতে ছেদ করে।
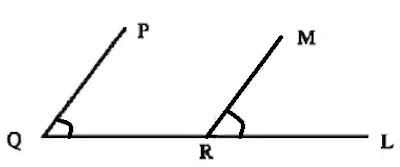
ফলে ∠PQR ও ∠MRL দুইটি অনুরুপ কোণ উৎপন্ন হয়।
এখন,
আমরা তিন কাঠির খেলা থেকে জানি,
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।
তাহলে, ∠PQR = ∠MRL
এখন শর্তানুসারে,
∠PQR = ৫৫° অর্থাৎ ∠MRL = ৫৫°
আবার,
প্রদত্ত চিত্র অনুসারে,
∠NRL = ∠NRM + ∠MRL = ৯০°
বা, ∠NRM + ∠MRL = ৯০°
বা, ∠NRM + ৫৫° = ৯০°
বা, ∠NRM = ৯০° – ৫৫°
বা, ∠NRM = ৩৫° [Ans.]
৩।
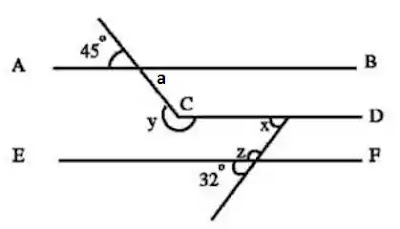
চিত্রে AB, CD ও EF পরস্পর সমান্তরাল।
(ক) কোণ z এর মান কত?
(খ) কোণ x এর মান কত?
(গ) কোণ y-z এর মান কত?
সমাধানঃ
(ক)
দুইটি কাঠি gh ও ij নেই এবং তাদেরকে নিচের চিত্র অনুসারে স্থাপন করে পর্যবেক্ষন করি।
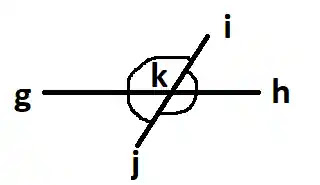
এখান থেকে দেখি, ∠gkj+∠ikg = এক সরলকোণ।
তাহলে, কাঠির পর্যবেক্ষন হতে প্রাপ্ত ফলাফলের মাধ্যমে আমরা প্রদত্ত চিত্র হতে বলতে পারি,
৩২°+∠z = এক সরলকোণ
বা, ∠z = এক সরলকোণ – ৩২°
বা, ∠z = ১৮০° – ৩২°
বা, ∠z = ১৪৮° [Ans.]
(খ)
এবার দুইটি কাঠিকে সমান্তরালে স্থাপন করে অপর একটি কাঠি এমনভাবে রাখি যেন সেটি সমান্তরাল কাঠিদ্বয়কে নিচের চিত্র অনুসারে ছেদ করে।
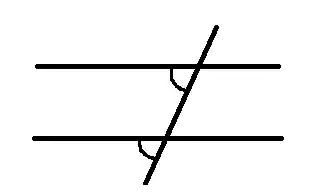
কাঠির এই স্থাপনকে পর্যবেক্ষন করে পাই,
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।
তাহলে, প্রদত্ত চিত্র হতে পর্যবেক্ষনকৃত জ্ঞান দ্বারা আমরা লিখতে পারি,
৩২° = ∠x [অনুরুপ কোণ]
অতএব, ∠x = ৩২° [Ans.]
(গ)
এবার দুইটি কাঠিকে সমান্তরালে স্থাপন করে অপর একটি কাঠি এমনভাবে রাখি যেন সেটি সমান্তরাল কাঠিদ্বয়কে নিচের চিত্র অনুসারে ছেদ করে। কাঠির এই স্থাপনকে পর্যবেক্ষন করে পাই,
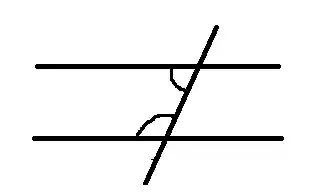
কাঠির এই স্থাপনকে পর্যবেক্ষন করে পাই,
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে ছেদকের একই পাশের অন্তঃস্থ কোণের পরিমাপের যোগফল দুই সমকোণের সমান হয়।
তাহলে, প্রদত্ত চিত্র হতে পর্যবেক্ষনকৃত জ্ঞান দ্বারা আমরা লিখতে পারি,
∠C + ∠a = ১৮০°
বা, ∠C + ৪৫° = ১৮০° [∠a এর বিপ্রতীপ ৪৫° বলে]
বা, ∠C = ১৮০°-৪৫°
বা, ∠C = ১৩৫°
আবার,
∠C + ∠y = চার সমকোণ
বা, ১৩৫° + ∠y = ৩৬০° [∠C এর প্রাপ্ত মান বসিয়ে]
বা, ∠y = ৩৬০° – ১৩৫°
বা, ∠y = ২২৫°
এখন,
প্রশ্ন অনুসারে,
∠y – ∠z
= ২২৫° – ১৪৮° [ক হতে z এর মান বসিয়ে]
= ৭৭° [Ans.]
ত্রিভুজের বৈশিষ্ট্য – ৫ম অধ্যায় ( ১১৮ – ১২৬ পৃষ্ঠা)
ত্রিভুজের বৈশিষ্ট্য
এই অধ্যায়ে আমরা তিনটি কাঠি দিয়ে একটি ক্ষেত্রকে আবদ্ধ করবো এবং এর বিভিন্ন বৈশিষ্ট্য নিয়ে আলোচনা করবো। তিনটি রেখাংশ দিয়ে যে ক্ষেত্রটিকে আবদ্ধ করা হয় তাকেই ত্রিভুজক্ষেত্র বলে এবং সেই ক্ষেত্রের সীমারেখাকে বলা হয় ত্রিভুজ (triangle)। এই অধ্যায় জুড়ে আমরা তিনটি কাঠিকে তিনটি রেখাংশ হিসেবে ধরে নিবো এবং বিভিন্ন প্রকার ত্রিভুজ তৈরি করবো। তারপর তার বিভিন্ন বৈশিষ্ট্য আমরা বিভিন্ন কার্যক্রর্যমের মাধ্যমে খুঁজে বের করবো এবং সেই বৈশিষ্ট্যগুলো প্রয়োগ করতে চেষ্টা করবো।
তিনিটি কাঠি নিয়ে ত্রিভুজ গঠনে শিখন ফলাফলঃ যেসকল ক্ষেত্রে আমরা ত্রিভুজ তৈরি করতে পেরেছি সেসব ক্ষেত্রে অবশ্যই ত্রিভুজের যেকোনো দুইটি বাহুর দৈর্ঘ্যের যোগফল তৃতীয় বাহুর দৈর্ঘ্যের চাইতে বেশি।
একক কাজ:
নিচের কোন কোন ক্ষেত্রে ত্রিভুজ আঁকা সম্ভব – ব্যাখ্যা দাও।
১। ১ সে.মি., ২ সে.মি. ও ৩ সে.মি.
২। ১ সে.মি., ২ সে.মি. ও ৪ সে.মি.
৩। ৪ সে.মি., ৫ সে.মি. ও ৭ সে.মি.
সমাধানঃ
আমরা জানি,
শুধুমাত্র ৩নং ক্ষেত্রে ত্রিভুজ গঠন করা সম্ভব।
ব্যাখ্যাঃ
আমরা জানি,
ত্রিভুজের দুইটি বাহুর দৈর্ঘ্যের যোগফল তৃতীয় বাহুর দৈর্ঘ্যের চাইতে বেশি হবে।
এখন,
১ নং ক্ষেত্রে,
১ সেমি + ২ সেমি = ৩ সেমি যা ৩য় দৈর্ঘ্য ৩ সেমি এর থেকে বেশি নয়।
২ নং ক্ষেত্রে,
১ সেমি + ২ সেমি = ৩ সেমি যা ৩য় দৈর্ঘ্য ৪ সেমি এর থেকে বেশি নয়।
৩ নং ক্ষেত্রে,
৪ সেমি + ৫ সেমি = ৯ সেমি যা ৩য় দৈর্ঘ্য ৭ সেমি এর থেকে বেশি।
সেইহেতু,
শুধুমাত্র ৩নং ক্ষেত্রে ত্রিভুজ গঠন করা সম্ভব।
কিছু শিখন ফলাফলঃ
- যেকোনো ত্রিভুজের তিনটি মধ্যমা সবসময় একটি নির্দিষ্ট বিন্দুতে ছেদ করে।
- ত্রিভুজের ওজন উক্ত বিন্দুতে কেন্দ্রীভুত থাকে, উক্ত বিন্দুকে ত্রিভুজের ভরকেন্দ্র বলে।
- কোণের সমদ্বিখন্ডক রেখা শীর্ষবিন্দুতে থাকা অন্তঃস্থ কোণটিকে সমান দুই ভাগে ভাগ করে।
কাজ: উপরে বর্ণিত উপায় ছাড়া আর কোন উপায়ে ত্রিভুজের বিপরীত বাহুর উপরে লম্ব আঁকার চেষ্টা করে দেখো।
বিঃদ্রঃ পাঠ্যবইয়ে ১২১ নং পৃষ্ঠায় কাগজ ভাঁজ করে কিভাবে ত্রিভুজের যেকোনো শীর্ষ হতে এর বিপরীত বাহুর উপর লম্ব আঁকা তার বর্ণনা করা হয়েছে। আমরা এখানে কাগজ ভাঁজ ছাড়া একটি পদ্ধতি দেখালাম।
সমাধানঃ
মনে করি, ত্রিভুজ ABC এর একটি শীর্ষবিন্দু A হতে এর বিপরীত বাহু BC এর উপর লম্ব আঁকতে হবে।
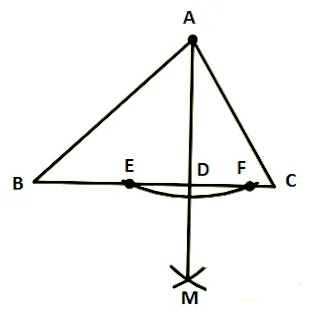
অঙ্কনঃ
ক) A কে কেন্দ্র করে এমন একটি ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা BC কে দুইটি বিন্দু E ও F বিন্দুতে ছেদ করে।
খ) E ও F কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে A এর বিপরীত দিকে দুইটি বৃত্তচাপ আঁকি যারা পরস্পরকে M বিন্দুতে ছেদ করে।
গ) A ও M যোগ করি যা BC কে D বিন্দুতে ছেদ করে। তাহলে AD-ই হলো নির্ণেয় অঙ্কিত লম্ব।
অনুশীলনীঃ
১। তোমাকে একটি ত্রিভুজ আঁকতে বলা হলো যার তিন বাহুর দৈর্ঘ্য ৪ সেমি, ৫ সেমি এবং ১০ সেমি। তুমি কি ত্রিভুজটি আঁকতে পারবে? আঁকা সম্ভব কি না তার কারণ একটি বাক্যে ব্যাখ্যা করো।
সমাধানঃ
না, আমি আঁকতে পারব না।
আঁকা সম্ভব না তার কারণ একটি বাক্যে ব্যাখ্যাঃ
যেহেতু ত্রিভুজের দুইটি বাহুর দৈর্ঘ্যের যোগফল ৪ সেমি+৫ সেমি=৯ সেমি, তৃতীয় বাহুর দৈর্ঘ্যে ১০ সেমির চাইতে বেশি নয়।
২। নিচের চিত্র থেকে কোণ x এর মান বের করো।

সমাধানঃ
আমরা জানি,
ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০° ।
তাহলে, চিত্র অনুসারে,
∠x+130°+20°=180°
বা, ∠x+150°=180°
বা, ∠x=180°-150°
বা, ∠x=30° [Ans.]
৩। নিচের চিত্র থেকে কোণ w এর মান বের করো।
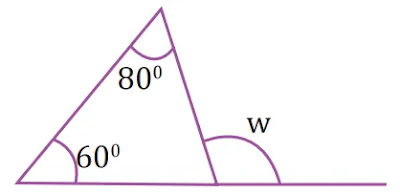
সমাধানঃ
আমরা জানি,
ত্রিভুজের তিনটি কোণের সমষ্টি 180°।
তাহলে, চিত্র অনুসারে,
১ম কোম+২য় কোণ+৩য় কোণ = 180°
বা, 60°+80°+৩য় কোণ = 180°
বা, 140° + ৩য় কোণ = 180°
বা, ৩য় কোণ = 180°-140°
বা, ৩য় কোণ = 40°
আবার,
ত্রিভুজের যে অন্তঃস্থ এবং বহিঃস্থ কোণগুলো সন্নিহিত (adjacent) তারা একে অপরের সম্পূরক কোণ।
তাহলে,
40°+∠w=180°
বা, ∠w =180°-40°
বা, ∠w = 140° [Ans.]
৪। চিত্রে কোণ x এর পরিমাপ কত?
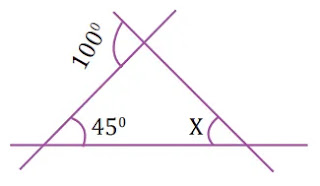
সমাধানঃ
আমরা জানি,
ত্রিভুজের যে অন্তঃস্থ এবং বহিঃস্থ কোণগুলো সন্নিহিত (adjacent) তারা একে অপরের সম্পূরক কোণ।
প্রদত্ত চিত্রে বহিঃস্থ একটি কোণটি 100°
তাহলে 100° কোণের সন্নিহিত অন্তঃস্থ কোণের মান = 180°-100° = 80° যা চিত্রের একটি কোণ।
এখন,
একটি ত্রিভুজের তিন কোণের সমষ্টি 180°।
তাহলে,
80°+45°+∠x = 180°
বা, 125°+∠x=180°
বা, ∠x = 180°-125°
বা, ∠x = 55° [Ans.]
৫। জয় একটি ত্রিভুজ এঁকেছে কিন্তু তার বাহুগুলোর পরিমাপ চিত্রের চেয়ে ভিন্ন। চিত্রে বসানো পরিমাপ দেখে বলতে হবে ত্রিভুজের বৃহত্তম কোণ কোনটি?
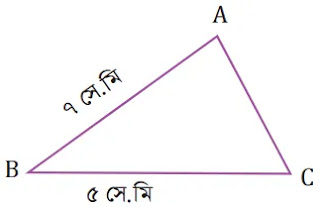
পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇
👉 সর্বসমতা ও সদৃশতা – ৬ষ্ঠ অধ্যায় – সমাধান | গণিত | সপ্তম শ্রেণী | Class 7 Math Chapter 6 | BD 2023

