এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর দশম অধ্যায়, নানা রকম আকৃতি মাপি, সম্পর্কে।
নানা রকম আকৃতি মাপি
আমরা পূর্বেই সমতল দ্বিমাত্রিক জ্যামিতি সম্পর্কে জেনেছি। নানা রকম আকৃতি মাপি এর এই অংশে আমরা সামন্তরিক, আয়ত, বর্গ, রম্বস, বৃত্ত, অর্ধবৃত্ত, ত্রিভুজের পরিসীমা ও ক্ষেত্রফল মাপা শিখব অর্থাৎ কিভাবে পরিসীমা ও ক্ষেত্রফল নির্ণয় করতে হয় তা জানব চিত্রসহকারে। এবং ট্রাপিজিয়ামের ক্ষেত্রফল কি কি ভাবে নির্ণয় করা যায় তার জন্য প্রদত্ত জোড়ায় কাজের সমাধান দিব ‘নানা রকম আকৃতি মাপি’ এর এই অংশে। প্রথমে ছক-১ ও ছক-২ দিয়ে আমরা শুরু করব।
নানা রকম আকৃতি মাপি এর ছক ১ ও ছক-২ এর সমাধানঃ
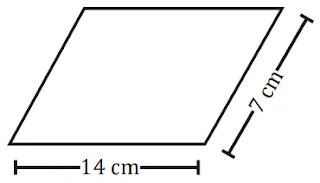
নামঃ সামন্তরিক
পরিসীমাঃ 2×(দুইটি সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টি) = 2×(14+7) সেমি = 2×21 সেমি = 42 সেমি
ক্ষেত্রফলঃ চিত্রে প্রয়োজনীয় তথ্য ক্ষেত্রফল নির্ণয়ের জন্য যথেষ্ট নয়।
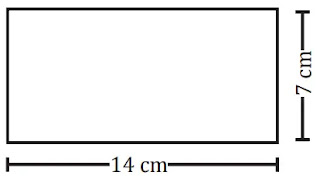
নামঃ আয়তক্ষেত্র
পরিসীমাঃ 2×(দুইটি সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টি) = 2×(14+7) সেমি = 2×21 সেমি = 42 সেমি
ক্ষেত্রফলঃ দৈর্ঘ্য×প্রস্থ = 14×7 বর্গ সেমি = 98 বর্গ সেমি
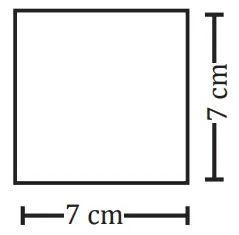
নামঃ বর্গক্ষেত্র
পরিসীমাঃ 4×এক বাহুর দৈর্ঘ্য = 4×7 সেমি = 28 সেমি
ক্ষেত্রফলঃ =(এক বাহুর দৈর্ঘ্য)2 = 72 বর্গ সেমি = 49 বর্গ সেমি
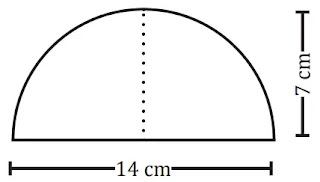
নামঃ অর্ধবৃত্ত
পরিসীমাঃ = π×ব্যাসার্ধ = π×7 সেমি = 3.1416×7 সেমি = 21.9912 সেমি।
ক্ষেত্রফলঃ ½× π×(ব্যাসার্ধ)2 = ½×π×72 বর্গ সেমি = ½×3.1416×49 বর্গ সেমি =76.9692 বর্গ সেমি।
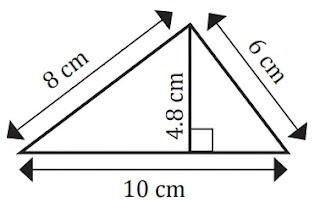
নামঃ ত্রিভুজ
পরিসীমাঃ তিন বাহুর সমষ্টি = (10+6+8) সেমি = 24 সেমি।
ক্ষেত্রফলঃ ½×ভুমি×উচ্চতা = ½×10×4.8 বর্গ সেমি = 24 বর্গ সেমি।
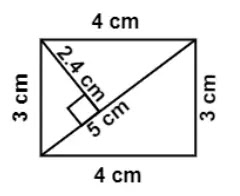
নামঃ আয়তক্ষেত্র
পরিসীমাঃ 2×(দুইটি সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টি) = 2(4+3) সেমি = 14 সেমি।
ক্ষেত্রফলঃ দৈর্ঘ্য×প্রস্থ = 4×3 বর্গ সেমি = 12 বর্গ সেমি।
ক্ষেত্রফলঃ 5×2.4 বর্গ সেমি = 12 বর্গ সেমি
[ব্যাখ্যাঃ চিত্রে আয়তের 5 সেমি কর্ণ একে দুইটি সমান ত্রিভুজ ক্ষেত্রে বিভক্ত করে, যেখানে একটি ত্রিভুজ ক্ষেত্রের ভুমি 5 সেমি ও উচ্চতা 2.4 সেমি, তাহলে এই ত্রিভুজের ক্ষেত্রফল = ½×5×2.4 বর্গ সেমি। এখন একটি ত্রিভুজের ক্ষেত্রফল = ½×5×2.4 বর্গ সেমি হলে দুইটি ত্রিভুজের ক্ষেত্রফল 5×2.4 বর্গ সেমি আর দুইটি ত্রিভুজ ক্ষেত্র মিলে প্রদত আয়তক্ষেত্র যার ক্ষেত্রফল 5×2.4 বর্গ সেমি ]
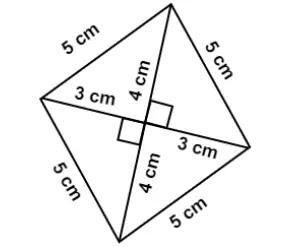
নামঃ রম্বস
পরিসীমাঃ 4×এক বাহুর দৈর্ঘ্য = 4×5 সেমি = 20 সেমি।
ক্ষেত্রফলঃ ½×কর্ণদ্বয়ের গুণফল = ½×(4+4)×(3+3) বর্গ সেমি = 24 বর্গ সেমি।
এবার মনে করো দৈর্ঘ্য ও প্রস্থের মান জানা নেই। তাহলে চলো দেখা যাক মান বসানোর পরিবর্তে দৈর্ঘ্য ও প্রস্থকে অজানা রাশি হিসাবে চলক দিয়ে প্রকাশ করে দেখি।
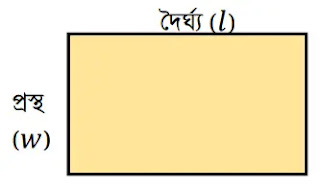
নামঃ আয়তক্ষেত্র
পরিসীমাঃ 2×(দুইটি সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টি) = 2(w+l) একক
ক্ষেত্রফল = দৈর্ঘ্য×প্রস্থ = wl বর্গ একক
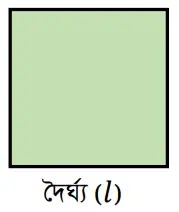
নামঃ বর্গ
পরিসীমাঃ 4×এক বাহুর দৈর্ঘ্য = 4l একক
ক্ষেত্রফল = (এক বাহুর দৈর্ঘ্য)2 = l2 বর্গ একক
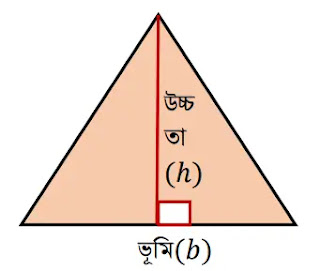
নামঃ ত্রিভুজ
পরিসীমাঃ ত্রিভুজের তিন বাহুর সমষ্টি = a+b+c একক [উল্লেখ্য প্রদত্ত চিত্রে সকল বাহুর দৈর্ঘ্যের উল্লেখ নেই]
ক্ষেত্রফলঃ ½×ভুমি×উচ্চতা = ½×b×h বর্গ একক
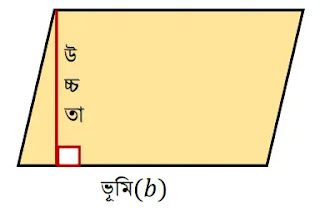
নামঃ সামন্তরিক
পরিসীমাঃ 2×(সন্নিহিত দুই বাহুর দৈর্ঘ্যের সমষ্টি) = 2(a+b) একক [উল্লেখ্য চিত্র a এর উল্লেখ নেই]
ক্ষেত্রফল = ভুমি×উচ্চতা = b×h বর্গ একক
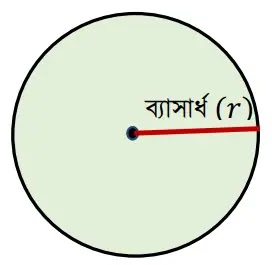
নামঃ বৃত্ত
পরিসীমাঃ 2πr [এখানে, π =3.14 ও r = ব্যাসার্ধ]
ক্ষেত্রফল = πr2 [এখানে, π =3.14 ও r = ব্যাসার্ধ]
শিখন সূত্রঃ
ট্রাপিজিয়ামের ক্ষেত্রফল = ½ × (সমান্তরাল বাহুদ্বয়ের সমষ্টি × উচ্চতা) বর্গ একক।
জোড়ায় কাজ: (১৯৭+১৯৮ পৃষ্ঠা)
কাগজ কেটে নিচের (ক), (খ) ও (গ) চিত্রের মতো মডেল তৈরি করো। তারপর বিকল্প একাধিক পদ্ধতিতে ক্ষেত্রফল নির্ণয় করো।
(ক) কাগজ কেটে আমরা নিচের চিত্র (ক) এর মত মডেল তৈরি করলাম এবং এর ক্ষেত্রফল নির্ণয় করলাম।
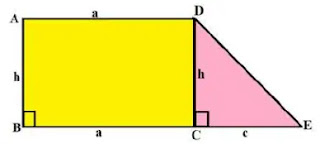
চিত্রে, ABED একটি ট্রাপিজিয়াম। D হতে BE এর উপর DC লম্ব। তাহলে DC হলো ট্রাপিজিয়ামের উচ্চতা। উল্লেখ্য এখানে, AB=DC=h, AD=BC=a, CE=c. DC ট্রাপিজিয়ামকে দুইটি ক্ষেত্র ABCD আয়ত ও DCE ত্রিভুজে বিভক্ত করে।
তাহলে,
ট্রাপিজিয়ামের ক্ষেত্রফল
= ABCD এর ক্ষেত্রফল + DCE এর ক্ষেত্রফল
= ah + ½×c×h
= ah + ½ch
= ½h(2a+c)
= ½h{a+(a+c)}
= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল।
(খ) এবার কাগজ কেটে একই মাপের দুইটি ট্রাপিজিয়াম নিয়ে নিচের চিত্রের মত পাশাপাশি রেখে একটি সামন্তরিক গঠন করি।
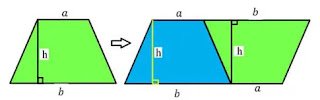
আমরা জানি,
সামন্তরিকের ক্ষেত্রফল=ভুমি×উচ্চতা
তাহলে,
আমাদের গঠিত সামন্তরিকের ক্ষেত্রফল
= (a+b)×h
এখন,
গঠিত সামন্তরিকের ক্ষেত্রফল একই মাপের দুইটি ট্রাপিজিয়াম দ্বারা গঠিত।
অতএব,
একটি ট্রাপিজিয়ামের ক্ষেত্রফল
= ½×(a+b)×h
= ½×h×(a+b)
= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল।
(গ) এবার কাগজ কেটে একটি ট্রাপিজিয়াম নিই। এরপর প্রথমে টাপিজিয়ামটিকে চিত্র অনুসারে মাঝ বরাবর আলাদা করি তাহলে এর উচ্চতা দুই অংশে ভাগ হয়ে গেল। পরবর্তিতে দুই ভাগকে চিত্রে উল্লেখিত পদ্ধতিতে বসাই। এবার প্রাপ্ত সামন্তরিকের ডান পাশের ত্রিভুজ অংশকে কেটে নিয়ে চিত্রানুসারে বাম পাশে স্থাপন করি ফলে আমরা একটি আয়তক্ষেত্র পেলাম। তাহলে এই আয়তক্ষেত্রের ক্ষেত্রফলই হলো ট্রাপিজিয়ামটির ক্ষেত্রফল।
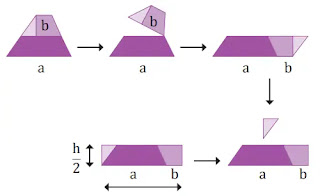
তাহলে, চিত্র অনুসারে,
ট্রাপিজিয়ামের ক্ষেত্রফল
= আয়তক্ষেত্রের ক্ষেত্রফল
= দৈর্ঘ্য×প্রস্থ
= (a+b)×h/2
= ½×h×(a+b)
= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল।
নানা রকম আকৃতি মাপি (ট্রাপিজিয়াম ও রম্বস)– ১০ম অধ্যায় (পৃষ্ঠা ১৯৮ – ২০০)
নানা রকম আকৃতি মাপি: ট্রাপিজিয়াম ও রম্বস
নানা রকম আকৃতি মাপি অধ্যায়ের এটি দ্বিতীয় অংশ যেখানে আমরা ১৯৮ – ২০০ পৃষ্ঠায় প্রদত্ত একক কাজ অর্থাৎ ট্রাপিজিয়ামের ক্ষেত্রফল ও পরিসীমা বিষয়ম সমস্যার সাথে রম্বসের ক্ষেত্রফল বিষয়ক সমস্যার ছক সমাধান করেছি। অর্থাৎ এই অধ্যায়ে থাকছে-
- গ্রাফ পেপারের উপর ট্রাপিজিয়াম অঙ্কন
- ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়
- ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য নির্ণয়
- ট্রাপিজিয়ামের ক্ষেত্রফল ও পরিসীমা যাচাইকরণ
- রম্বসের ক্ষেত্রফল নির্ণয়
- রমবসের কর্ণের দৈর্ঘ্য নির্ণয়
একক কাজ:
১. গ্রাফ পেপারের উপর একটি ট্রাপিজিয়াম আঁক। প্রতিটি ক্ষুদ্রতম বর্গকে 1 বর্গ একক এবং আংশিক ক্ষুদ্রতম অংশকে 0.5 বর্গ একক ধরে ট্রাপিজিয়ামটির ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
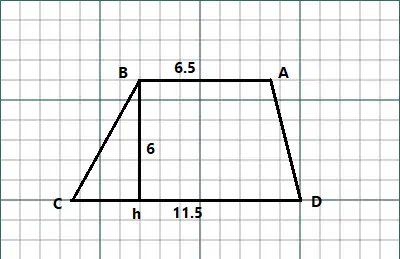
একটি গ্রাফ পেপার নিই এবং এর উপর একটি ট্রাপিজিয়াম ABCD অঙ্কন করি যার AB || CD. এখন প্রতিটি ক্ষুদ্রতম বর্গকে 1 বর্গ একক এবং আংশিক ক্ষুদ্রতম অংশকে 0.5 বর্গ একক ধরে এর উচ্চতা ও সমান্তরাল দুই বাহুর দৈর্ঘ্য নির্ণয় করি।
তাহলে আমরা পাই,
AB = 6.5 একক
CD = 11.5 একক
উচ্চতা, Bh = 6 একক
এখন,
ট্রাপিজিয়ামের ক্ষেত্রফল
= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল
= ½×6×(6.5+11.5) বর্গ একক
= ½×6×18 বর্গ একক
= 54 বর্গ একক.
২. একটি ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির দৈর্ঘ্যের অন্তর 8 সেন্টিমিটার এবং এদের লম্ব দূরত্ব 24 সেন্টিমিটার। যদি ট্রাপিজিয়ামটির ক্ষেত্রফল 312 বর্গ সেন্টিমিটার হয়, তবে এর সমান্তরাল বাহু দুইটির দৈর্ঘ্য নির্ণয় করো।
সমাধানঃ
মনে করি, ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির মধ্যে ছোট বাহুর দৈর্ঘ্য = a সেমি
তাহলে, ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির মধ্যে বড় বাহুর দৈর্ঘ্য = a+8 সেমি
আমরা জানি,
ট্রাপিজিয়ামের ক্ষেত্রফল = ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল
তাহলে,
312 = ½×24×(a+a+8) [যেহেতু, দেওয়া আছে, উচ্চতা 24 সেমি ও ক্ষেত্রফল 312 সেমি]
বা, 312 = 12×(2a+8)
বা, 2a+8 = 312/12
বা, 2a+8 = 26
বা, 2a = 26-8
বা, 2a = 18
বা, a = 18/2
বা, a = 9
অর্থাৎ, সমান্তরাল এক বাহু = 9 সেমি
তাহলে, সমান্তরাল অপর বাহু = 9+8 সেমি = 17 সেমি।
৩. চিত্রে ΔBCE এর ক্ষেত্রফল 100 বর্গ সেন্টিমিটার হলে, ABCD ট্রাপিজিয়ামটির ক্ষেত্রফল নির্ণয় করো।
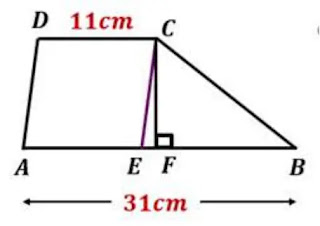
সমাধানঃ
চিত্র হতে পাই,
AD || CE অর্থাৎ, DC = AE.
এখন,
AB = 31
বা, AE + EB = 31
বা, DC + EB = 31 [DC = AE বলে]
বা, 11 + EB = 31
বা, EB = 31 – 11
বা, EB = 20 সেমি
এখন দেওয়া আছে,
ΔBCE এর ক্ষেত্রফল = 100 বর্গ সেমি
বা, ½×EB×CF = 100 [এখানে, ভুমি = EB, উচ্চতা = CF]
বা, EB×CF = 200
বা, 20×CF = 200 [মান বসিয়ে]
বা, CF = 10 সেমি
এখন,
ট্রাপিজিয়ামটির ক্ষেত্রফল
= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল
= ½×CF×(AB+DC)
= ½×10×(31+11)
= 5×42
= 210 বর্গ সেমি।
৪. নিচের ট্রাপিজিয়াম দুইটির ক্ষেত্রফল নির্ণয় করো:
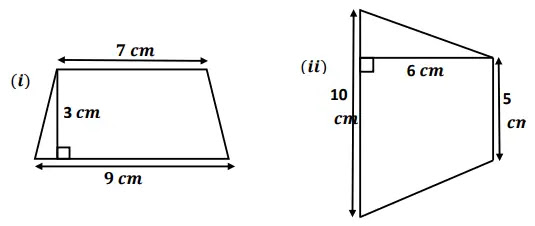
সমাধানঃ
১ নং ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ঃ
দেওয়া আছে,
চিত্র হতে দেখি, চিত্রটির আকৃতির প্রতিটি বাহু সমান এবং সমান্তরাল ফলে এদের নামের ঘরে রম্বস লিখলাম।
১ম চিত্রের, ক্ষেত্রফল = ½×কর্ণদ্বয়ের গুণফল = ½×8×12 বর্গ সেমি= 48 বর্গ সেমি
২য় চিত্রের QS বা ২য় কর্ণটির দৈর্ঘ্য নির্ণেয়; রম্বসের সূত্রমতে আমরা লিখতে পারি,
½×PR×QS = 42
বা, PR×QS = 84
বা, 6×QS = 84
বা, QS = 14 সেমি।
পরবর্তী পৃষ্ঠার সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

