
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর দ্বিতীয় অধ্যায় বীজগাণিতিক রাশির সূচক, গুণ ও তাদের প্রয়োগ (৪১ – ৫২ পৃষ্ঠা), সম্পর্কে।
একক কাজঃ সূচকের শূন্য বিধি (zero exponent), ঋণাত্মক সূচক (negative exponent) বিধি অনুসারে নিচের রাশিগুলোকে সরল করো।
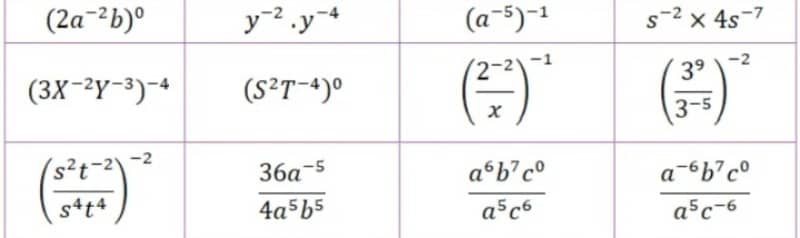
সমাধানঃ
(2a-2b)0
= 20×a-2×0.b0
= 1.a0.1
= 1.1.1
= 1
y-2 .y-4
= y-2-4
= y-6
(a-5)-1
= a-5×-1
= a5
s-2×4s-7
= 4.s-2-7
= 4s-9
4
= —-
s9
(3x-2y-3)-4
= 31×-4.x-2×-4.y-3×-4
= 3-3.x8.y12
(S2T-4)0
= S2×0.T-4×0
= S0.T0
= 1.1
= 1
(2-2/x)-1
2-2×-1
= ——-
x-1
22
= ——-
1/x
= 22x
= 4x
(39/3-5)-2
(39)-2
= ——-
(3-5)-2
39×-2
= ——-
3-5×-2
3-18
= ——
310
= 3-18-10
= 3-28
1
= —–
328
(s2t-2/s4t4)-2
s2×-2.t-2×-2
= ———–
s4×-2.t4×-2
s-4.t4
= ——-
s-8.t-8
= s-4+8.t4+8
= s4t12
36a-5
——
4a5b5
9.a-5-5
= ——-
b5
9.a-10
= ——-
b5
9
= ——-
a10b5
a6b7c0
——–
a5c6
= a6-5b7c0-6
= a1b7c-6
ab7
= ——
c6
a-6b7c0
———
a5c-6
= a-65b7c0+6
= a-11b7c6
b7c6
= —–
a11
বীজগণিতীয় রাশির গুণ (Algebraic Multiplication)
সাধারন গুণ আর বীজগণিতীয় রাশির গুণ এর মধ্যে একটু ভিন্নতা আছে। বীজগণিতে গুণের ক্ষেত্রে আমরা সংখ্যার আগে অবস্থিত চিহ্নেরও গুণ করে থাকি যা নিন্মোক্ত সিদ্ধান্ত অনুসারে করা হয়।
1. (+1).(+1)=+1
2. (+1).(-1)=-1
3. (-1).(+1)=-1
4. (-1).(-1)=+1
লক্ষ করি:
# একই চিহ্নযুক্ত দুইটি রাশির গুণফল (+) চিহ্নযুক্ত হবে।
# বিপরীত চিহ্নযুক্ত দুইটি রাশির গুণফল (-) চিহ্নযুক্ত হবে।
কাগজ কেটে গুণ
একক কাজঃ কাগজ কেটে গুণ করোঃ 2x+y-1, 3x
সমাধানঃ
(১) গুণফল নির্ণয়ের জন্য কাগজ কেটে +1, -1, +y, -y, +x, -x, +xy, -xy, +x2 ও –x2 এর জন্য টাইলস বানাই।
(২) এবার কাগজে কলাম বরাবর 2x+y-1 এবং সারি বরাবর 3x এর উপাদানের টাইলস চিত্র অনুযায়ী বসাই। অতপর, কলাম অংশের প্রত্যেক টাইলস দিয়ে সারির অংশের প্রত্যেক টাইলসকে গুণ করে সারি-কলামের সমন্ময় ক্ষেত্রে গুণফল এর টাইলস বসাই।
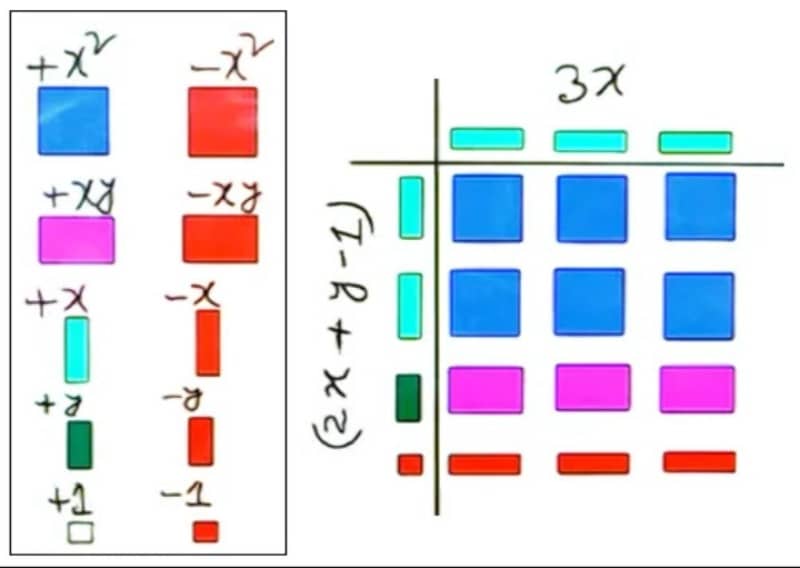
(৩) সমন্ময় ক্ষেত্রে অবস্থিত সব টাইলসগুলো যোগ করি। যোগের পর ক্ষেত্রফল পাই = 6x2 + 3xy -3y
অতএব, নির্ণেয় গুণফলঃ 6x2 + 3xy -3x
একক কাজঃ কাগজ কেটে গুণ করোঃ (x+3)(x+4)
(১) গুণফল নির্ণয়ের জন্য কাগজ কেটে +1, -1, +x, -x, +x2 ও –x2 এর জন্য টাইলস বানাই।
(২) এবার কাগজে কলাম বরাবর x+3 এবং সারি বরাবর x+4 এর উপাদানের টাইলস চিত্র অনুযায়ী বসাই। অতপর, কলাম অংশের প্রত্যেক টাইলস দিয়ে সারির অংশের প্রত্যেক টাইলসকে গুণ করে সারি-কলামের সমন্ময় ক্ষেত্রে গুণফল এর টাইলস বসাই।
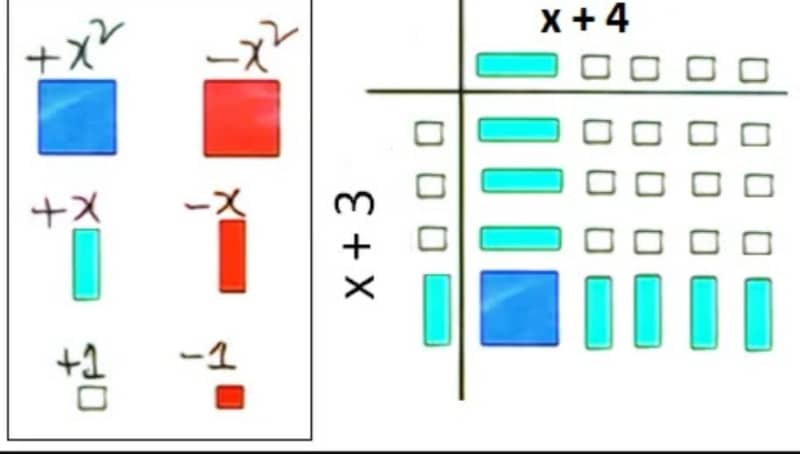
(৩) সমন্ময় ক্ষেত্রে অবস্থিত সব টাইলসগুলো যোগ করি। যোগের পর ক্ষেত্রফল পাই = x2 + 7x + 12
অতএব, নির্ণেয় গুণফলঃ x2 + 7x + 12
একক কাজঃ কাগজ কেটে গুণ করো (2x+1)(x-2)
সমাধানঃ
(১) গুণফল নির্ণয়ের জন্য কাগজ কেটে +1, -1, +x, -x, +x2 ও –x2 এর জন্য টাইলস বানাই।
(২) এবার কাগজে কলাম বরাবর 2x+1 এবং সারি বরাবর x-2 এর উপাদানের টাইলস চিত্র অনুযায়ী বসাই। অতপর, কলাম অংশের প্রত্যেক টাইলস দিয়ে সারির অংশের প্রত্যেক টাইলসকে গুণ করে সারি-কলামের সমন্ময় ক্ষেত্রে গুণফল এর টাইলস বসাই।
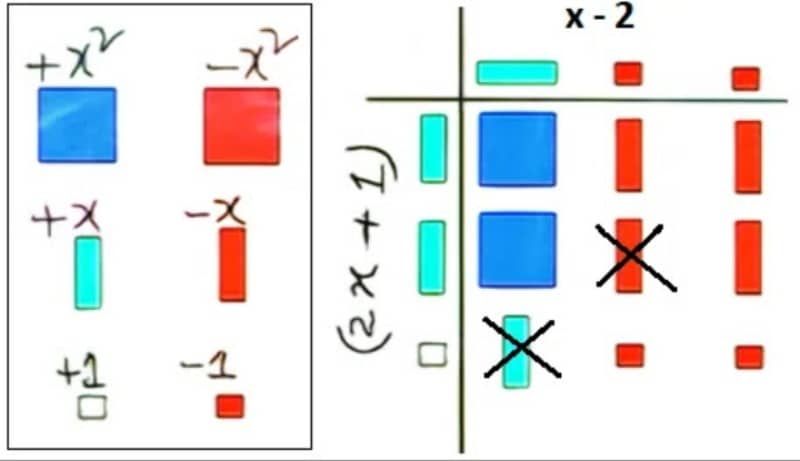
(৩) সমন্ময় ক্ষেত্রে অবস্থিত সব টাইলসগুলো যোগ করি (বিপরিত চিহ্নযুক্ত একই টাইলস ক্রস দিয়ে বাদ দেই)। যোগের পর ক্ষেত্রফল পাই = 2x2 – 3x – 2
অতএব, নির্ণেয় গুণফলঃ 2x2 – 3x – 2
একক কাজঃ
১. কাগজ কেটে গুনফল নির্ণয় করোঃ (x+2)(3x-2)
সমাধানঃ
(ক) গুণফল নির্ণয়ের জন্য কাগজ কেটে +1, -1, +x, -x, +x2 ও –x2 এর জন্য টাইলস বানাই।
(খ) এবার কাগজে কলাম বরাবর x+2 এবং সারি বরাবর 3x-2 এর উপাদানের টাইলস চিত্র অনুযায়ী বসাই। অতপর, কলাম অংশের প্রত্যেক টাইলস দিয়ে সারির অংশের প্রত্যেক টাইলসকে গুণ করে সারি-কলামের সমন্ময় ক্ষেত্রে গুণফল এর টাইলস বসাই।
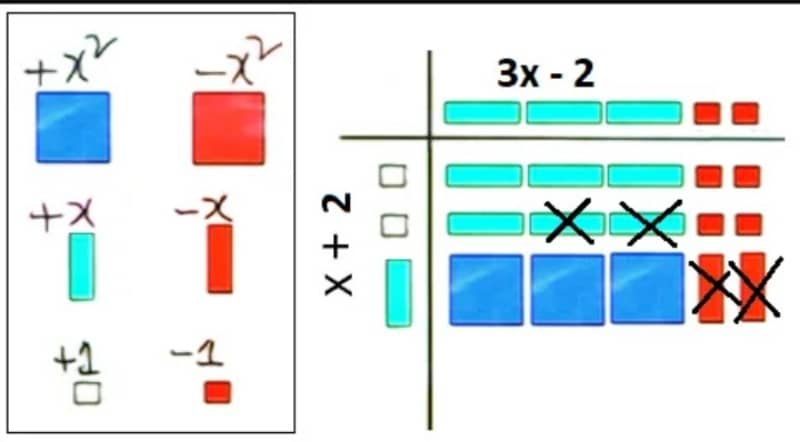
(গ) সমন্ময় ক্ষেত্রে অবস্থিত সব টাইলসগুলো যোগ করি (বিপরিত চিহ্নযুক্ত একই টাইলস ক্রস দিয়ে বাদ দেই)। যোগের পর ক্ষেত্রফল পাই = 3x2 + 4x – 4
অতএব, নির্ণেয় গুণফলঃ 3x2 + 4x – 4
২. নিচের চিত্রটির ক্ষেত্রফল নির্ণয় করোঃ
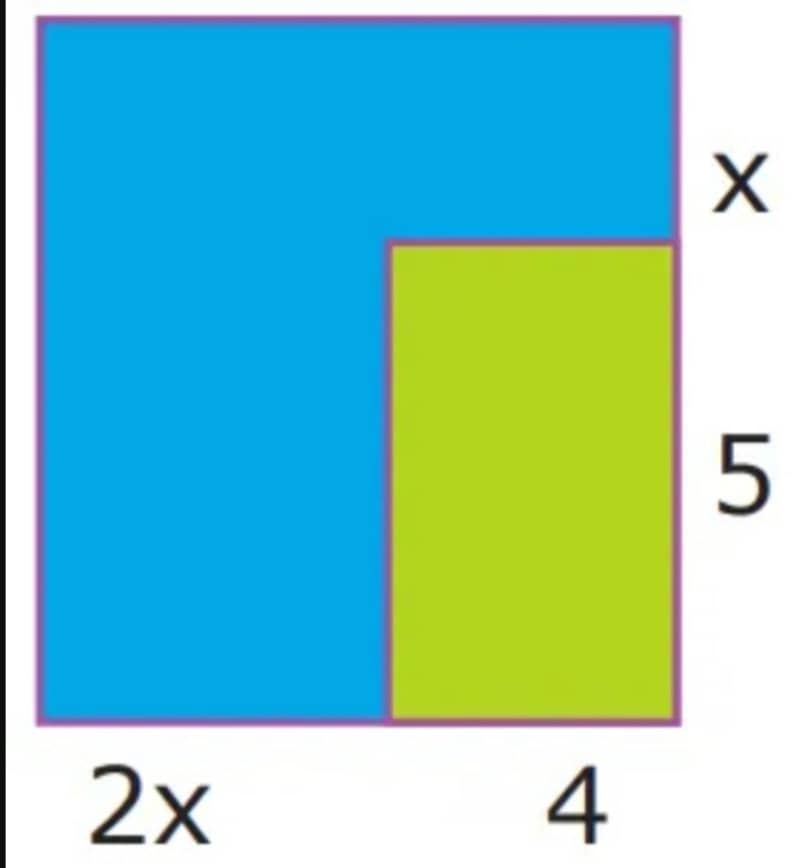
সমাধানঃ
নিচের চিত্রের দৈর্ঘ্য = 2x+4 এবং প্রস্থ = x+5
অতএব,
চিত্রটির ক্ষেত্রফল
= (2x+4)(x+5)
= 2x2+4x+10x+20
= 2x2+14x+20
৩. সূত্রের সাহায্যে গুণফল নির্ণয় করোঃ
I. (x+y)(x-y)(x2+y2)
II. (a+1)(a-1)(a2+1)
III. (x2+xy+y2)(x-y)
সমাধানঃ
I. (x+y)(x-y)(x2+y2)
= (x2-y2)(x2+y2) [a2-b2=(a+b)(a-b) সূত্র অনুসারে]
= (x2)2-(y2)2
= x4-y4
II. (a+1)(a-1)(a2+1)
= (a2-12)(a2+1)
= (a2-12)(a2+12)
= (a2)2-(12)2
= a4-14
= a4 – 1
III. (x2+xy+y2)(x-y)
= (x-y)(x2+xy+y2)
= x3-y3
৪. নিচের চিত্রের আয়তন নির্ণয় করো।
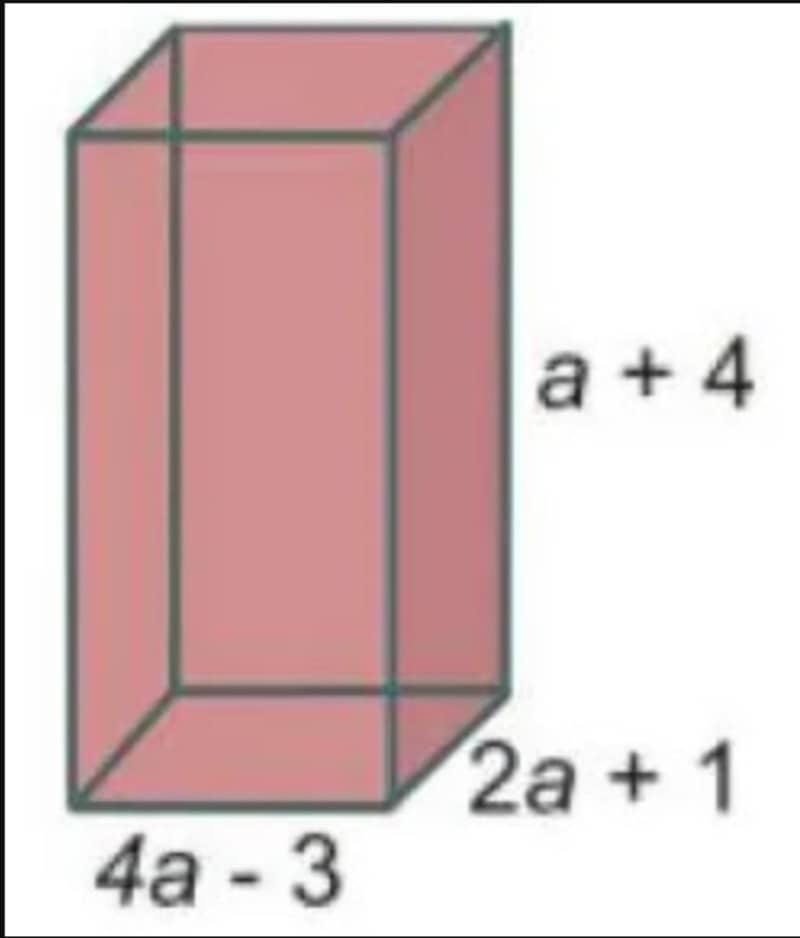
সমাধানঃ
চিত্র হতে পাই,
এর দৈর্ঘ্য = 4a-3
প্রস্থ = 2a+1
উচ্চতা = a+4
অতএব,
চিত্রটির আয়তন
= (4a-3)(2a+1)(a+4)
= (8a2-6a+4a-3)(a+4)
= (8a2-2a-3)(a+4)
= 8a3-2a2-3a+32a2-8a-12
= 8a3+30a2-11a-12
৫. নিচের চিত্রটির ক্ষেত্রফল নির্ণয় করোঃ
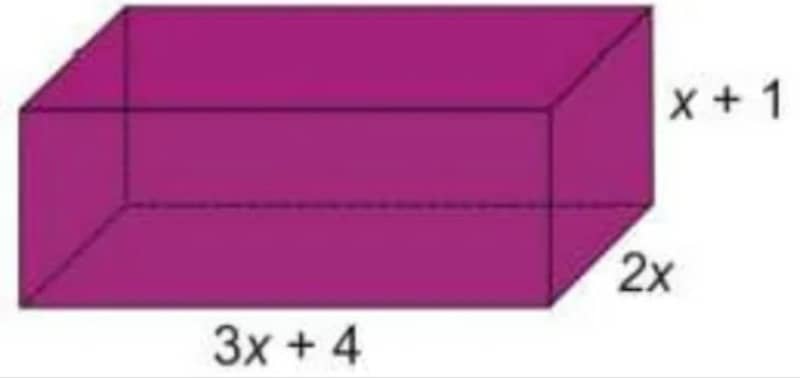
সমাধানঃ
চিত্রটি একটি আয়তাকার ঘনবস্তু।
চিত্রটির দৈর্ঘ্য a = 3x+4, প্রস্থ b = 2x, উচ্চতা c = x+1
আমরা জানি,
আয়তাকার ঘনবস্তুর ক্ষেত্রফল = 2(ab+bc+ca)
তাহলে,
চিত্রটির ক্ষেত্রফল
= 2(ab+bc+ca)
= 2{(3x+4)2x + 2x(x+1) + (x+1)(3x+4)}
= 2{(6x2+8x) + (2x2+2x) + (3x2+3x+4x+4)}
= 2{(6x2+8x) + (2x2+2x) + (3x2+7x+4)}
= 2(11x2+17x+4)
= 22x2+34x+8
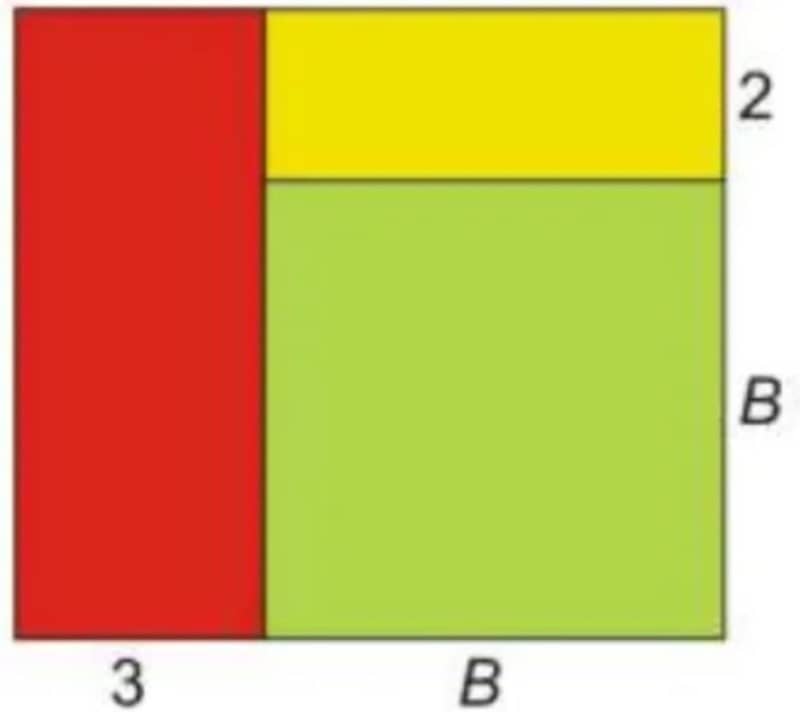
৬. নিচের চিত্রটির আয়তন নির্ণয় করোঃ
সমাধানঃ
প্রদত্ত চিত্রের দৈর্ঘ্য = B+3 এবং প্রস্থ = B+2
কিন্তু চিত্রটির উচ্চতা দেওয়া নাই।
তাহলে, আমরা চিত্রটির আয়তন বের করতে পারবো না।
যদি ক্ষেত্রফল বের করতে বলে, তবে এর ক্ষেত্রফল
= দৈর্ঘ্য×প্রস্থ
= (B+3)(B+2)
= B2+3B+2B+6
= B2+5B+6
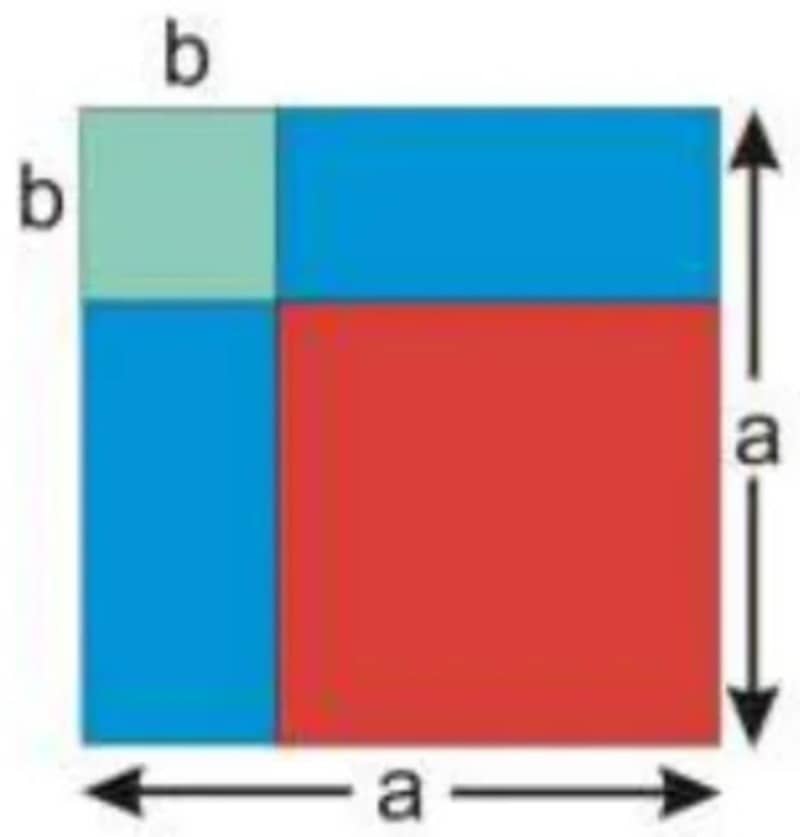
৭. নিচের চিত্রটির লাল রংয়ের ক্ষেত্রটির ক্ষেত্রফল নির্ণয় করো:
সমাধানঃ
দেওয়া আছে,
চিত্রটির দৈর্ঘ্য = a এবং প্রস্থ = a
এবং সবচেয়ে ছোট ক্ষেত্রটির দৈর্ঘ্য = b এবং প্রস্থ = b
উপরের তথ্য চিত্র হতে পর্যালোচনা করে পাই,
চিত্রটির লাল রংয়ের ক্ষেত্রটির দৈর্ঘ্য = a-b এবং প্রস্থ = a-b
তাহলে,
চিত্রটির লাল রংয়ের ক্ষেত্রটির ক্ষেত্রফল
= (a-b)2
= a2-2ab+b2
পরবর্তী পৃষ্ঠার সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

