এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর দ্বাদশ অধ্যায়, বীজগাণিতিক রাশির সমীকরণ, সম্পর্কে।

অজানা রাশির সমীকরণ

আমরা ৬ষ্ঠ শ্রেণিতে সমীকরণ ও সরল সমীকরণ সম্পর্কে জেনে এসেছি এবং বাস্তবভিত্তিক সমস্যা থেকে সমীকরণ গঠন করতে শিখেছি। সপ্তম শ্রেণির এই অধ্যায়ে আমরা সমীকরণ সমাধানের কিছু বিধি ও প্রয়োগ সম্পর্কে জানব। ৬ষ্ঠ শ্রেণিতে আমরা সরল সমীকরণ সমাধানের জন্য কতগুলো নিয়ম শিখেছিলাম। চলো নিয়ম গুলোর বাস্তব প্রমান করতে চেষ্টা করি। আমরা আমাদের এই অধ্যায়ে অজানা রাশির সমীকরণ কীভাবে পাই তার বাস্তব প্রমান দেখব। তাহলে শুরু করা যাকঃ-

বাস্তব সমস্যায় অজানা রাশির সমীকরণ

# নিচের নির্দেশিত ভারসাম্য থেকে অজানা মানগুলো কী হতে পারে তা চিন্তা করো এবং ফলাফল খাতায় লিখ।

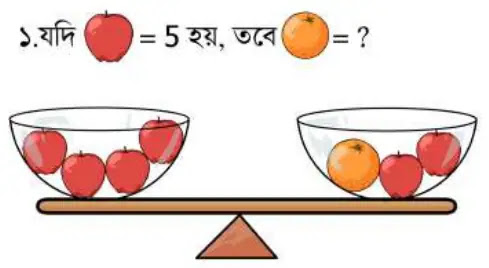
সমাধানঃ

১নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

4টি আপেল = 1টি কমলা লেবু + 2টি আপেল

বা, 4×5 =  1টি কমলা লেবু + 2×5 [শর্তমতে]

বা, 20 = 1টি কমলা লেবু + 10

বা, 1টি কমলা লেবু + 10 = 20

বা, 1টি কমলা লেবু + 10 – 10 = 20 – 10 [উভয়পক্ষ থেকে 10 বিয়োগ করে]

বা, 1টি কমলা লেবু = 10

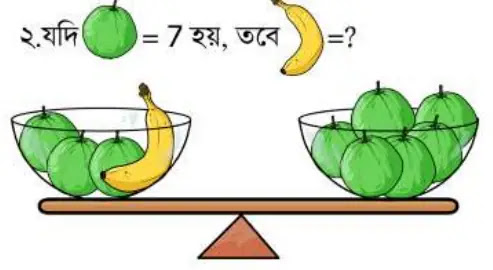
২নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

3 টি পেয়ারা + 1 টি কলা = 6 পেয়ারা

বা, 3টি পেয়ারা + 1 টি কলা – 3টি পেয়ারা  = 6টি পেয়ারা – 3টি পেয়ারা [উভয়পক্ষ থেকে 3টি পেয়ারা বিয়োগ করে]

বা, 1 টি কলা = 3টি পেয়ারা

বা, 1 টি কলা = 3×7

বা, বা, 1 টি কলা = 21

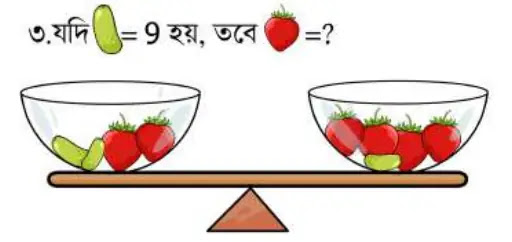
৩নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

2টি শসা + 2টি স্ট্রবেরি = 4টি স্ট্রবেরি + 1টি শসা

বা, 2টি শসা + 2টি স্ট্রবেরি – 1টি শসা = 4টি স্ট্রবেরি + 1টি শসা – 1টি শসা [উভয়পক্ষ থেকে 1টি শসা বিয়োগ করে]

বা, 1টি শসা + 2টি স্ট্রবেরি = 4টি স্ট্রবেরি

বা, 1টি শসা + 2টি স্ট্রবেরি – 2টি স্ট্রবেরি = 4টি স্ট্রবেরি – 2টি স্ট্রবেরি [উভয়পক্ষ থেকে 2টি স্ট্রবেরি বিয়োগ করে]

বা, 1টি শসা = 2টি স্ট্রবেরি

বা, 1টি শসা = 2টি স্ট্রবেরি

বা, 2টি স্ট্রবেরি = 1টি শসা

বা, 2টি স্ট্রবেরি = 9 [মান বসিয়ে]

বা, 1টি স্ট্রবেরি = ⁹/₂ [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, 1টি স্ট্রবেরি = 4.5

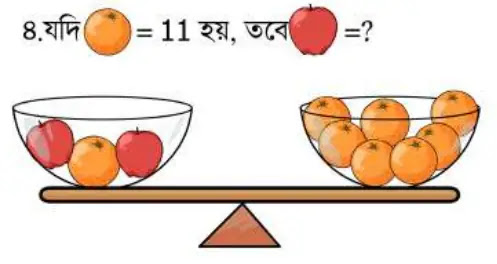
৪নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

2টি আপেল + 1টি কমলা লেবু = 7টি কমলা লেবু

বা, 2টি আপেল + 1টি কমলা লেবু – 1টি কমলা লেবু = 7টি কমলা লেবু – 1টি কমলা লেবু [[উভয়পক্ষ থেকে 1টি কমলা লেবু বিয়োগ করে]]

বা, 2টি আপেল = 6টি কমলা লেবু

বা, 1টি আপেল = 3টি কমলা লেবু [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, 1টি আপেল = 3×11

বা, 1টি আপেল = 33

ভারসাম্য সমীকরণ:

একটি সমীকরণের ভারসাম্য বজায় রাখা হবে যদি আমরা :

● উভয় পাশে একই পরিমাণ যোগ করি।

● উভয় পাশ থেকে একই পরিমাণ বিয়োগ করি।

● উভয় পাশকে একই পরিমাণ দিয়ে গুণ করি।

● উভয় পাশকে একই পরিমাণ দিয়ে ভাগ করি।

কাজ:

পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির পরিবর্তীত সমীকরণ বের করো এবং গুণ ও ভাগের বিধি নির্ণয় করো।

ক) সমীকরণটির সাথে 3 যোগ করা হয়

খ) সমীকরণটি থেকে 3 বিয়োগ করা হয়

গ) 4 দ্বারা গুণ করা হয়

ঘ) 2 দ্বারা ভাগ করা হয়

সমাধানঃ

ক) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির সাথে 3 যোগ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি। এক্ষেত্রে, প্রিতিটি ধনাত্মক সংখ্যার জন্য পাল্লায় ওজন (●) বৃত্ত সংখ্যা বসাই।

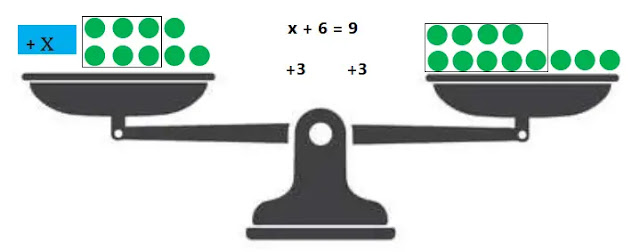
ওজন (●) ব্যবহারের গাণিতিক ধাপসমূহঃ

x + 6 = 9

বা, x + 6 + 3 = 9 + 3

বা, x + 9 = 12

অর্থাৎ, সমীকরণটির সাথে 3 যোগ করা হলে পরিবর্তীত সমীকরণঃ x + 9 = 12

(খ) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির থেকে 3 বিযোগ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি। এক্ষেত্রে, প্রিতিটি ধনাত্মক সংখ্যার জন্য পাল্লায় ওজন (●) বৃত্ত সংখ্যা ও ঋণাত্মক সংখ্যার জন্য ওজন (●) বৃত্ত সংখ্যা বসাই।

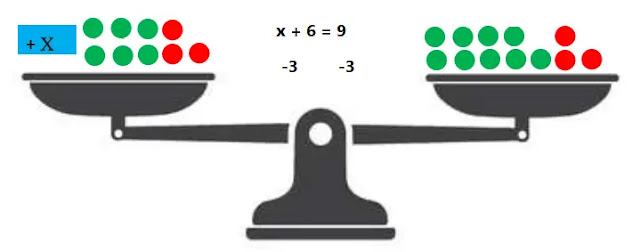
ওজন (●) ও (●) ব্যবহারের গাণিতিক ধাপসমূহঃ

x + 6 = 9

বা, x + 6 – 3 = 9 – 3

বা, x + 3 = 6

অর্থাৎ, সমীকরণটির থেকে 3 বিযোগ করা হলে পরিবর্তীত সমীকরণঃ x + 3 = 6

(গ) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটিকে 4 দ্বারা গুণ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি।

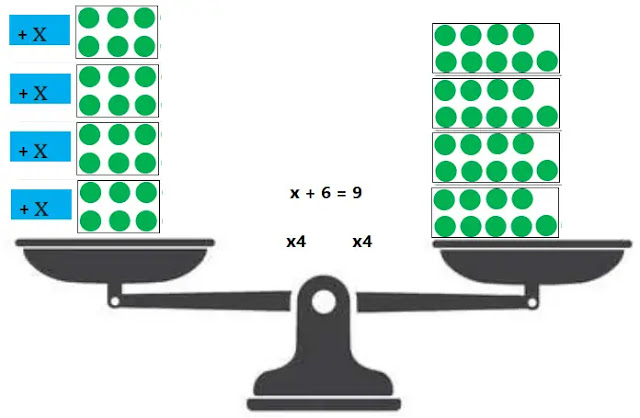
4 দ্বারা গুণ করার গাণিতিক ধাপসমূহঃ

x + 6 = 9

বা, 4(x + 6) = 4×9

বা, 4x + 24 = 36

অর্থাৎ, সমীকরণটিকে 4 দ্বারা গুণ করা হলে পরিবর্তীত সমীকরণঃ 4x + 24 = 36

(ঘ) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটিকে 2 দ্বারা ভাগ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি।

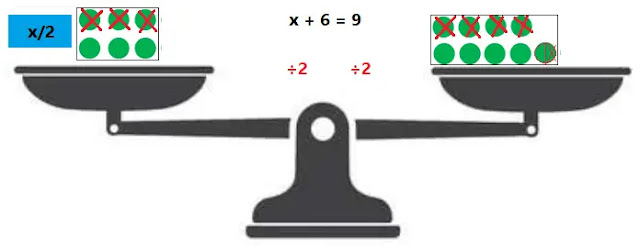
2 দ্বারা ভাগ করার গাণিতিক ধাপসমূহঃ

x + 6 = 9

বা, (x + 6) ÷2 = 9÷2

বা, ^x/₂ + ⁶/₂ = ⁹/₂

বা, ^x/₂ + 3 = ⁹/₂

অর্থাৎ, সমীকরণটিকে 4 দ্বারা গুণ করা হলে পরিবর্তীত সমীকরণঃ ^x/₂ + 3 = ⁹/₂

আজানা রাশির সমীকরণ বিধি – Class 7 Math BD 2023 – দ্বাদশ অধ্যায় (২৩১ পৃষ্টা একক কাজ)

 আজানা রাশির সমীকরণ বিধি

আমরা আজানা রাশির সমীকরণ বিধি অংশে (অধ্যায় ১২শ এর) ২৩১ পৃষ্ঠার একক কাজ এর সমাধান করব। এখানে যোগ, বিয়োগ, গুণ, ভাগ সংক্রান্ত কিছু বিধি দ্বারা কিভাবে সমীকরণ গঠণ করা যায় তা দেখানো হয়েছে। তাহলে শুরু করা যাকঃ-

পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে নিচের সমীকরণগুলোর পরিবর্তীত সমীকরণ নির্ণয় করো। সমীকরণগুলো পর্যবেক্ষণ করে কোন ক্ষেত্রে যোগের বর্জন বিধি, গুণের বর্জন বিধি, আড়গুণন বিধি, প্রতিসাম্য বিধি ব্যবহার করা যাবে সে সম্পর্কে সিদ্ধান্ত দাও।

একক কাজ:

২। 7x + 5 = 25 থেকে 7x = 20

৩। 5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1

৪। ^3x/₂ = ⁷/₄ = থেকে 12x = 14

৫। 5x + 2 = 7x – 4 থেকে 7x – 4 = 5x + 2

২ নং এর সমাধানঃ

7x + 5 = 25 থেকে 7x = 20

পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 ব্যবহার করে সমীকরণ 7x + 5 = 25 এর ভারসাম্য নির্ণয় করি। অতপর 7x + 5 = 25 থেকে 7x = 20 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

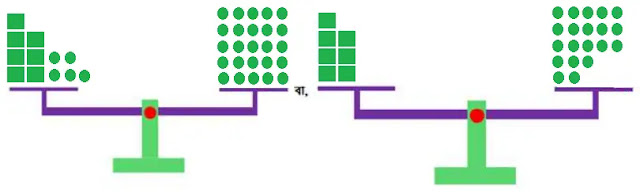
পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

7x + 5 = 25

বা, 7x + 5 – 5 = 25 – 5 [উভয়পক্ষ থেকে 5 বিয়োগ করি]

বা, 7x = 20

অর্থাৎ, এই প্রক্রিয়ায় যোগের বর্জন বিধি ব্যবহার করা যাবে।

৩ নং এর সমাধানঃ

5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1

পাল্লায় ওজন-বাটখাড়া হিসেবে (3x+2) এর জন্য 🟩, (2x+1) এর জন্য 🟢 ব্যবহার করে সমীকরণ 5(3x + 2) = 5(2x +1) এর ভারসাম্য নির্ণয় করি। অতপর 5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

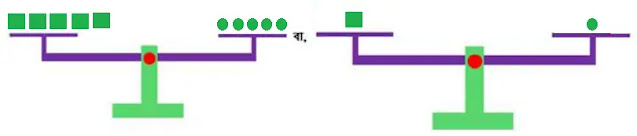
পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

5(3x + 2) = 5(2x +1)

বা, (3x + 2) = (2x +1) [উভয়পক্ষকে 5 দ্বারা ভাগ বা 5 বর্জন করে]

অর্থাৎ, এই প্রক্রিয়ায় গুণের বর্জন বিধি ব্যবহার করা যাবে।

৪ নং এর সমাধানঃ

^3x/₂ = ⁷/₄ = থেকে 12x = 14

এখানে,

^3x/₂ = ⁷/₄

বা, ^4×3x/₂ = ^4×7/₄ [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 6x = 7

এখন,

পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 ব্যবহার করে সমীকরণ 6x = 7 এর ভারসাম্য নির্ণয় করি। অতপর 6x = 7 থেকে 12x = 14 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

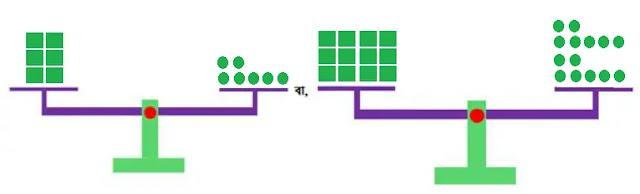
পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

6x = 7

বা, 2×6x = 2×7 [উভয়পক্ষ 2 দ্বারা গুণ করি]

বা, 12x = 14

এখন, এই সমগ্র প্রক্রিয়াটিকে আমরা নিন্মোক্তভাবে সহজীকরণ করে দেখাতে পারিঃ-

^3x/₂ = ⁷/₄

বা, 3x×4 = 7×2 [আড়গুণন করে]

বা, 12x = 14

অর্থাৎ, এই প্রক্রিয়ায় আড়গুণন বিধি ব্যবহার করা যাবে।

৫ নং এর সমাধানঃ

5x + 2 = 7x – 4 থেকে 7x – 4 = 5x + 2

পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 এবং -1 এর জন্য 🔴 ব্যবহার করে সমীকরণ 5x + 2 = 7x – 4 এর ভারসাম্য নির্ণয় করি। অতপর 5x + 2 = 7x – 4 থেকে 7x – 4 = 5x + 2 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

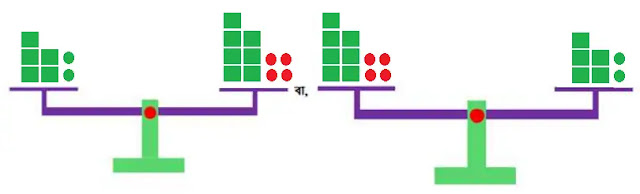
পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

5x + 2 = 7x – 4

বা, 7x – 4 = 5x + 2 [পক্ষান্তর করে]

অর্থাৎ, এই প্রক্রিয়ায় প্রতিসাম্য বিধি ব্যবহার করা যাবে।

দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ – Class 7 Math BD 2023 – দ্বাদশ অধ্যায় (২৩৪ ও ২৩৬ পৃষ্ঠা)

দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ

অজানা রাশির সমীকরন অধ্যায়ের এই অংশে আমরা ২৩৪ পৃষ্ঠা ও ২৩৬ পৃষ্ঠার দাঁড়িপাল্লার ভারসাম্য্য ও আদর্শ সমীকরণ বিষয়ক সমস্যার সমাধান করেছি। নিচে সমস্যার সমাধানসমূহ দেয়া হলোঃ

একক কাজ (২৩৪ পৃষ্ঠা)

দাঁড়িপাল্লার ভারসাম্যের সাহায্যে নিচের সমীকরণগুলো সমাধান করে দেখাও।

১. কোন সংখ্যার দ্বিগুণের বা দুইগুণের সাথে 5 যোগ করলে যোগফল 25 হবে?

২. দুইটি সংখ্যার যোগফল 55 এবং বড় সংখ্যাটির 5 গুণ ছোট সংখ্যাটির 6 গুণের সমান। সংখ্যা দুইটি নির্ণয় করো।

৩. গী তা, রি তা এবং মি তা র একত্রে 180 টাকা আছে। রিতার চেয়ে গী তা র 6 টাকা কম ও মি তা র 12 টাকা বেশি আছে। কার কত টাকা আছে?

সমাধানঃ

১নং এর সমাধানঃ

মনে করি, একটি সংখ্যা x

তাহলে x এর দ্বিগুনের সাথে 5 যোগ করলে হয় 2x+5

প্রশ্নমতে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় 2x+5 ও অন্য পাল্লায় 25 রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি। 

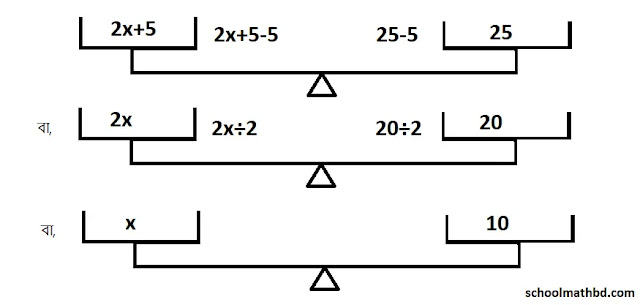
অতএব, সংখ্যাটি = 10

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

2x+5 = 25

বা, 2x+5-5 = 25-5 [উভয়পক্ষ থেকে 5 বিয়োগ করে]

বা, 2x = 20

বা, 2x÷2 = 20÷2 [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, x = 10

অতএব, সংখ্যাটি = 10

২নং এর সমাধানঃ

মনে করি, বড় সংখ্যাটি x

তাহলে, ছোট সংখ্যাটি = (55-x)

প্রশ্নমতে,

5x = 6(55-x)

তাহলে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় 5x ও অন্য পাল্লায় 6(55-x) রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি।

অতএব, বড় সংখ্যাটি = 30

এবং ছোট সংখ্যাটি = (55-30) = 25

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

5x = 6(55-x)

বা, 5x = 330-6x

বা, 5x+6x = 330

বা, 11x = 330

বা, ^11x/₁₁ = ³³⁰/₁₁ [উভয়পক্ষকে 11 দ্বারা ভাগ করে]

বা, x = 30

অতএব, বড় সংখ্যাটি = 30

এবং ছোট সংখ্যাটি = (55-30) = 25

৩নং এর সমাধানঃ

মনে করি, রিতার আছে x টাকা

তাহলে, গীতার আছে x-6 টাকা এবং মিতার আছে (x+12) টাকা।

প্রশ্নমতে,

x+(x-6)+(x+12) = 180

তাহলে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় x+(x-6)+(x+12)  ও অন্য পাল্লায় 180 রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি।

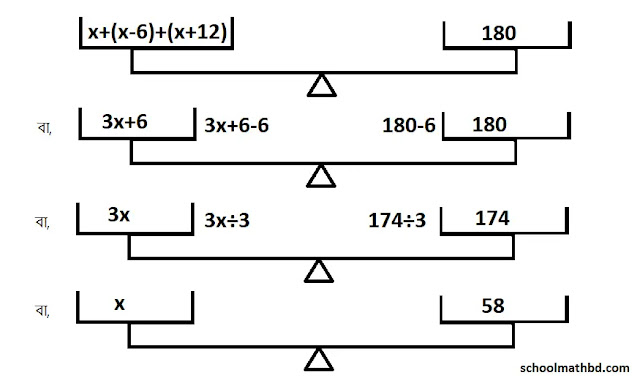
অতএব, রিতার আছে 58 টাকা

গীতার আছে (58-6) টাকা = 52 টাকা

মিতার আছে (58+12) টাকা = 70 টাকা।

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

x+(x-6)+(x+12) = 180

বা, 3x+6 = 180

বা, 3x+6-6 = 180-6 [উভয়পক্ষ থেকে 6 বিয়োগ করে]

বা, 3x = 174

বা, ^3x/₃ = ¹⁷⁴/₃ [উভয়পক্ষকে 3 দ্বারা ভাগ করে]

বা, x = 58

অতএব, রিতার আছে 58 টাকা

গীতার আছে (58-6) টাকা = 52 টাকা

মিতার আছে (58+12) টাকা = 70 টাকা।

একক কাজ: (পৃষ্টা ২৩৬)

আদর্শ সমীকরণ ax² + bx + c = 0 আকারে লিখ এবং a, b, c এর মান খুঁজে বের করো।

(i) 3x-2x²=7

সমাধানঃ

3x-2x²=7

বা, 3x-2x²-7=0

বা, -2x²+3x-7=0

বা, 2x²-3x+7=0

অতএব, আদর্শ আকার: 2x²-3x+7=0

এবং a,b,c = 2, -3, 7

(ii) (x-7)(x+7)=3x

সমাধানঃ

(x-7)(x+7)=3x

বা, x²-7x+7x-49=3x

বা, x²-49=3x

বা, x²-49-3x=0

বা, x²-3x-49=0

অতএব, আদর্শ আকার: x²-3x-49=0

এবং a,b,c = 1, -3, -49

(iv) 5+2z²=6z

সমাধানঃ

5+2z²=6z

বা, 5+2z²-6z=0

বা, 2z²-6z+5=0

অতএব, আদর্শ আকার: 2z²-6z+5=0

এবং a,b,c = 2, -6, 5

(v) 2x(x-3)=15

সমাধানঃ

2x(x-3)=15

বা, 2x²-6x=15

বা, 2x²-6x-15=0

অতএব, আদর্শ আকার:  2x²-6x-15=0

এবং a,b,c = 2, -6, -15

(vi) 5w(7w-2)=10w+1

সমাধানঃ

5w(7w-2)=10w+1

বা, 35w²-10w=10w+1

বা, 35w²-10w-10w-1=0

বা, 35w²-20w-1=0

অতএব, আদর্শ আকার:  35w²-20w-1=0

এবং a,b,c = 35, -20, -1

(vi) 4y-3y(y)=9

সমাধানঃ

4y-3y(y)=9

বা, 4y-3y²=9

বা, 4y-3y²-9=0

বা, -3y²+4y-9=0

বা, 3y²-4y+9=0

অতএব, আদর্শ আকার:  3y²-4y+9=0

এবং a,b,c = 3, -4, 9

(vii) a+2a²-19=5a²

সমাধানঃ

a+2a²-19=5a²

বা, a+2a²-19-5a²=0

বা, a-3a²-19=0

বা, -3a²+a-19=0

বা, 3a²-a+19=0

অতএব, আদর্শ আকার:  3a²-a+19=0

এবং a,b,c = 3, -1, 19

দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান – Class 7 Math BD 2023 – দ্বাদশ অধ্যায় (২৪১ পৃষ্ঠা)

দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান

প্রিয় সহযোগী, আমরা এই পাঠে অজানা রাশির সমীকরণ অধ্যায়ের ২৪১ পৃষ্ঠার প্রদত্ত সস্যাগুলোর সমাধান করব। এই অংশে আমরা দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান প্রক্রিয়া দেখাব। এখানে মোট ছয়টি সমস্যা দেয়া আছে, আমরা প্রত্যেকটির সমাধান চিত্র সহ দিয়েছি। আশা করি এটি দ্বারা আপনারা উপকৃত হবেন। আসুন শুরু করা যাক-

একক কাজঃ

দ্বিঘাত সমীকরণ গঠন করো এবং কাগজ কেটে সমাধান করো।

১. দুই অঙ্কবিশিষ্ট কোনো সংখ্যার অঙ্কদ্বয়ের সমষ্টি 15 এবং এদের গুণফল 56; সংখ্যাটি কত?

সমাধানঃ

মনে করি,

একক স্থানীয় অঙ্ক x

∴ দশক স্থানীয় অঙ্ক (15-x)

∴ সংখ্যাটি 

= 10(15-x)+x

= 150-10x+x

= 150-9x

শর্তমতে,

x(15-x) = 56

বা, 15x-x² = 56

বা, 15x-x²-56 = 0

বা, x²-15x+56 = 0

এখন,

সমীকরণ x²-15x+56 = 0 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি।

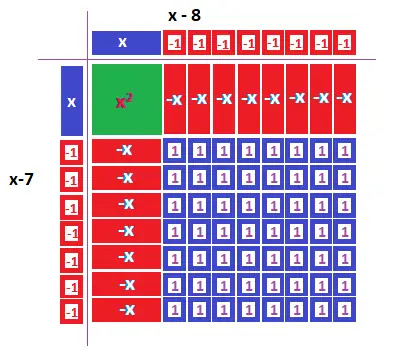
গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-7)(x-8)

সুতরাং,

(x-7)(x-8) = 0

বা, x-7 = 0 অথবা, x-8 = 0

বা, x = 7 অথবা, x = 8

তাহলে,

x=7 হলে, সংখ্যাটি = 150-9*7 = 150 – 63 = 87

এবং, x=8 হলে, সংখ্যাটি = 150-9*8 = 150 – 72 = 78

২. একটি আয়তাকার ঘরের মেঝের ক্ষেত্রফল 192 বর্গমিটার। মেঝের দৈর্ঘ্য 4 মিটার কমালে ও প্রস্থ 4 মিটার বাড়ালে ক্ষেত্রফল অপরিবর্তিত থাকে। মেঝের দৈর্ঘ্য ও প্রস্থ নির্ণয় করো।

সমাধানঃ

মনে করি,

আয়তাকার ঘরের মেঝের দৈর্ঘ্য = x মিটার

∴ আয়তাকার ঘরের মেঝের প্রস্থ = ¹⁹²/_x মিটার

শর্তমতে,

(x-4)( ¹⁹²/_x +4) = x*¹⁹²/_x

বা, (x-4)( ¹⁹²/_x +4) = 192

বা, (x-4)(192+4x) = 192x [উভয়পক্ষকে x দ্বারা গুণ করে]

বা, 192x-768+4x²-16x = 192x

বা, -768+4x²-16x = 0

বা, -192+x²-4x = 0 [উভয়পক্ষকে 4 দ্বারা ভাগ করে]

বা, x²-4x-192 = 0

বা, x²-4x = 192

বা, x²-4x+4 = 192+4 [উভয়পক্ষের সাথে 4 যোগ করে]

বা, x²-4x+4 = 196

এখন,

সমীকরণ x²-4x+4 = 196 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে x²-4x+4 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

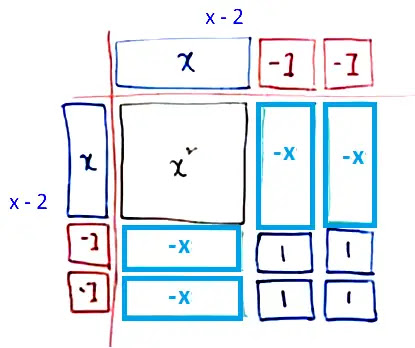
গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-2)(x-2)

সুতরাং,

(x-2)(x-2) = 196

বা, (x-2)² = 196

বা, x-2 = ±14 [বর্গমূল করে]

বা, x = ±14+2

বা, x= 14+2 = 16 অথবা, x = -14+2 = -12 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

তাহলে,

x=16

সুতরাং,

আয়তাকার ঘরের মেঝের দৈর্ঘ্য = 16 মিটার

এবং আয়তাকার ঘরের মেঝের প্রস্থ = ¹⁹²/₁₆ মিটার = 12 মিটার।

৩. একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য 15 সে.মি. ও অপর বাহুদ্বয়ের দৈর্ঘ্যের অন্তর 3 সে.মি.। ঐ বাহুদ্বয়ের দৈর্ঘ্য নির্ণয় করো।

সমাধানঃ

মনে করি,

সমকোণী ত্রিভুজের সমকৌণিক বৃহত্তম বাহুর দৈর্ঘ্য = x সেমি

∴ সমকোণী ত্রিভুজের সমকৌণিক ক্ষুদ্রত্তম বাহুর দৈর্ঘ্য = (x-3) সেমি।

তাহলে, পীথাগোরাসের উপপাদ্য অনুযায়ী,

x²+(x-3)² = 15²

বা, x²+x²-6x+9 = 225

বা, 2x²-6x+9-225 = 0

বা, 2x²-6x-216 = 0

বা, x²-3x-108 = 0

বা, x²-3x = 108

বা, 4x²-12x = 432 [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 4x²-12x+9 = 432+9 [উভয়পক্ষের সাথে 9 যোগ করে]

বা, 4x²-12x+9 = 441

এখন,

সমীকরণ 4x²-12x+9 = 441এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে 4x²-12x+9 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

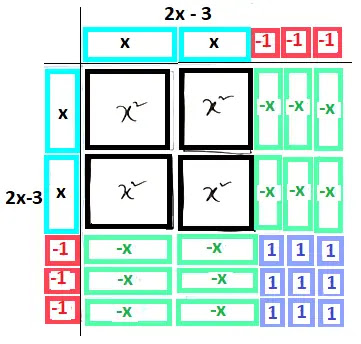
গঠিত ক্ষেত্রের ক্ষেত্রফল

= (2x-3)(2x-3)

অর্থাৎ,

(2x-3)(2x-3) = 441

বা, (2x-3)² = 441

বা, 2x-3 = ±21 [বর্গমূল করে]

বা, 2x = ±21+3

বা, 2x = 21+3 অথবা, 2x = -21+3

বা, 2x = 24 অথবা, 2x = -18 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

বা, x = 12

তাহলে,

একটি বাহু 12  সেমি এবং অপর বাহু (12-3) সেমি = 9 সেমি।

৪. একটি ত্রিভুজের ভূমি তার উচ্চতার দ্বিগুণ অপেক্ষা 6 সে.মি. বেশি। ত্রিভুজ ক্ষেত্রটির ক্ষেত্রফল 810 বর্গ সে.মি. হলে, এর উচ্চতা কত?

সমাধানঃ

মনে করি,

ত্রিভুজটির উচ্চতা = x সেমি

∴ ত্রিভুজটির ভূমি = 2x+6 সেমি

শর্তমতে,

½*(2x+6)*x = 810 [ যেহেতু, ত্রিভুজের ক্ষেত্রফল = ½*ভুমি*উচ্চতা  ]

বা, (2x+6)x = 1620 [উভয়পক্ষকে 2 দ্বারা গুণ করে]

বা, 2x²+6x = 1620

বা, x²+3x – 810 = 0

এখন,

সমীকরণ x²+3x – 810 = 0এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +3, -3, +9, -9 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি।

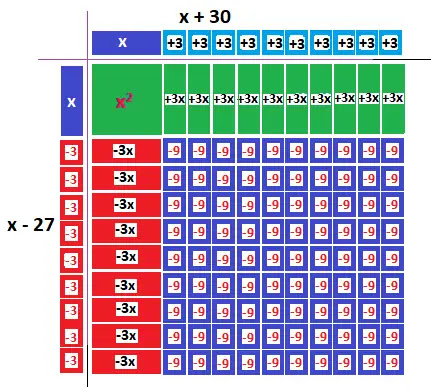
গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-27)(x+30)

তাহলে,

(x-27)(x+30) = 0

বা, x-27 = 0 অথবা, x+30 = 0

বা, x = 27 অথবা, x = -30 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

অতএব, ত্রিভুজটির উচতা 30 সেমি।

৫. একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে প্রত্যেকে তার সহপাঠীর সংখ্যার সমান টাকা চাঁদা দেওয়ায় মোট 420 টাকা চাঁদা উঠল। ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা কত এবং প্রত্যেকে কত টাকা করে চাঁদা দিল?

সমাধানঃ

মনে করি,

ছাত্র ছাত্রীর সংখ্যা x জন

∴ প্রত্যেকে চাঁদা দেয় (x-1) টাকা

∴ মোট চাঁদার পরিমাণ x(x-1) টাকা

শর্তমতে,

x(x-1) = 420

বা, x²-x = 420

বা, 4x²-4x = 1680 [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 4x²-4x+1 = 1680+1 [উভয়পক্ষের সাথে 1 যোগ করে]

বা, 4x²-4x+1 = 1681

এখন,

সমীকরণ 4x²-4x+1 = 1681 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে 4x²-4x+1 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

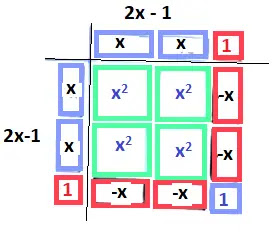
গঠিত ক্ষেত্রের ক্ষেত্রফল

= (2x-1)(2x-1)

= (2x-1)²

অতএব,

(2x-1)² = 1681

বা, 2x-1 = ±41

বা, 2x = ±41 +1

বা, 2x = 41+1 অথবা, 2x = -41+1

বা, 2x = 42 অথবা, 2x = -40

বা, x = 21  অথবা, x = -20 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

তাহলে,

ছাত্র ছাত্রীর সংখ্যা 21 জন

এবং প্রত্যেকে চাঁদা দেয় (21-1) টাকা = 20 টাকা।

৬. একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে প্রত্যেকে তত পয়সার চেয়ে আরও 30 পয়সা বেশি করে চাঁদা দেওয়াতে মোট 70 টাকা উঠল। ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা কত?

সমাধানঃ

মনে করি,

শিক্ষার্থীর সংখ্যা x জন

প্রত্যেকে চাদা দেয় (x+30) পয়সা

∴ মোট চাঁদার পরিমাণ = x(x+30) পয়সা

শর্তমতে,

x(x+30) = 70*100  [70 টাকাকে 100 দিয়ে গুণ করে পয়সা করা হয়েছে]

বা, x²+3x = 7000

বা, x²+3x +225 = 7000 + 225

বা, x²+3x +225 = 7225

এখন,

সমীকরণ x²+3x +225 = 7225 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x², +5x, +5 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে x²+3x +225 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x+15)(x+15)

= (x+15)²

অতএব,

(x+15)² = 7225

বা, x+15 = ±85

বা, x = ±85 -15

বা, x = 85 – 15 অথবা, x = -85 -15

বা, x = 70  অথবা, x = -100 [শিক্ষার্থীর সংখ্যা ঋণাত্মক হতে পারে না]

সুতরাং, ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা 70 জন।

পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

👉 তথ্য অনুসন্ধান ও বিশ্লেষণ  – ১৩ অধ্যায়- সমাধান | গণিত | সপ্তম শ্রেণী | Class 7 Math Chapter 13 | BD 2023