এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর চতুর্থ অধ্যায় অনুপাত, সমানুপাত, সম্পর্কে।

অনুপাত (Ratio)

সাধারণত দুইটি রাশির তুলনা করতে অনুপাত বা Ratio ব্যবহৃত হয় যেখানে একটি রাশি অপরটি থেকে কতগুণ ছোট বা বড় বা কতটুকু তা বোঝা যায়। একে : গাণিতিক চিহ্ন দ্বারা প্রকাশ করা হয়। যেমনঃ নয়ন এর মাসিক বেতন ১০০০০ টাকা ও দীদারের মাসিক বেতন ৩০০০০ টাকা। তাহলে, নয়ন ও দীদারের বেতনের অনুপাত = ১০০০০ : ৩০০০০ = ১ : ৩।

অর্থাৎ অনুপাত  ১ : ৩ থেকে বুঝি, দীদারের বেতন নয়নের থেকে বেশি এবং তা ৩ গুণ বেশি।

বিভিন্ন প্রকারের অনুপাত বিদ্যমান। class 7 math bd এর ৮৮ পৃষ্ঠার একক কাজটি সমাধানের ছক এর মাধ্যমে বিভিন্ন প্রকার অনপাতের ধারণা নিচে দেওয়া হলোঃ

১. অনুপাত সংক্রান্ত নিচের ছকটি পূরণ করোঃ

সমাধানঃ

অনুপাতের নাম	সম্পর্ক	উদাহরণ
সরল অনুপাত	দুইটি রাশি থাকবে।	৩:৫
লঘু অনুপাত	সরল অনুপাতের পূর্ব রাশি, উত্তর রাশি থেকে ছোট হবে।	৫:৮
গুরু অনুপাত	সরল অনুপাতের পূর্ব রাশি, উত্তর রাশি থেকে বড় হবে।	৮:৫
একক অনুপাত	সরল অনুপাতের পূর্ব রাশি ও উত্তর রাশি সমান হবে।	৫:৫ = ১:১
ব্যস্ত অনুপাত	কোন সরল অনুপাতের পূর্ব রাশিকে উত্তর রাশি এবং উত্তর রাশিকে পূর্ব রাশি করা হবে।	৩:৫ এর ব্যস্ত অনুপাত ৫: ৩।
বহুরাশিক অনুপাত	তিন বা ততোধিক রাশি থাকবে।	৩:৫:৮
ধারাবাহিক অনুপাত	দুটি অনুপাতের মধ্যে প্রথম অনুপাতের উত্তর রাশি ও দ্বিতীয় অনুপাতের পূর্ব রাশি পরস্পর সমান হবে।	৩:৫ ও ৫:৮ পরস্পর ধারাহিক অনুপাত।

কাজঃ পৃষ্ঠা ৮৬

১. এবার ভেবে দেখো, তোমাদের বইয়ের প্রস্থ ও পুরুত্বের জন্য যে দুটি অনুপাত পেয়েছিলে, সেই অনুপাত দুটি কোন ধরণের অনুপাত হবে? তোমার আশেপাশে উপরে শেখা ৩ ধরণের অনুপাতের আলাদা আলাদা ১ টি উদাহরণ খজেুঁ বের করো তো।

সমাধানঃ

আমার বয়ের প্রস্থ তার পুরুত্ব থেকে বড় ছিল। তাই বইয়ের প্রস্থ ও পুরুত্বের জন্য প্রাপ্ত অনুপাতটি গুরু অনুপাত ছিল।

আমার আশে পাশে উপরে শেখা (পাঠ্যপুস্তকে উল্লেক্ষিত) অনুপাতের উদাহরণঃ

ক. গুরু অনুপাতের উদাহরণঃ

আমার টেবিলের দৈর্ঘ্য : আমার টেবিলের প্রস্থ

= ৫৪:৩৬

= ৩:২

খ. লঘু অনুপাতের উদাহরণঃ

আমার বয়স বছর : আমার বন্ধুর বয়স

= ১০ বছর : ১১ বছর

= ১০:১১

গ. একক অনুপাতের উদাহরণঃ

গণিতে নয়নের প্রাপ্ত নম্বর : গণিতে দীদারের প্রাপ্ত নম্বর

= ৯০:৯০

=১:১

কাজ: ভেবে দেখতো ‘ব্যস্ত অনুপাত’ এবং ‘বিপরীত ভগ্নাংশ’ এর মধ্যে কোন মিল খজেুঁ পাও কিনা?

সমাধানঃ

হ্যাঁ, ব্যস্ত অনুপাত ও বিপরীত ভগ্নাংশের মধ্যে নিন্মোক্ত মিল খুঁজে পাইঃ

সরল অনুপাতকে ব্যস্ত অনুপাতে রুপান্তর করলে প্রাপ্ত অনুপাতের ভগ্নাংশের আকার সরল অনুপাতের ভগ্নাংশের আকারের বিপরীত ভগ্নাংশ।

উদাহরনঃ

২:৩ এর ব্যস্ত অনুপাত = ৩:২

আবার,

২:৩ = ^২/_৩

৩:২ = ^৩/_২

অর্থাৎ, ^২/_৩ এর বিপরীত ভগ্নাংশ ^৩/_২

কাজ: তোমার তিনটি বইয়ের দৈর্ঘ্য, প্রস্থ ও পুরুত্বের অনুপাত কী হবে?

সমাধানঃ

আমার তিনটি বইয়ের দৈর্ঘ্য, প্রস্থ ও পুরুত্বের মাপ নিন্মরুপঃ

	দৈর্ঘ্য	প্রস্থ	পুরুত্ব
গণিত বই	২৪.৩ সেমি	১৮.৫ সেমি	১.৫ সেমি
বাংলা বই	২৪.৩ সেমি	১৮.৫ সেমি	১ সেমি
ইংরেজি বই	২৪.৩ সেমি	১৮.৫ সেমি	১ সেমি

অতএব,

গণিত বইয়ের দৈর্ঘ্য, প্রস্থ ও পুরুত্বের অনুপাত = ২৪.৩ : ১৮.৫ : ১.৫

বাংলা বইয়ের দৈর্ঘ্য, প্রস্থ ও পুরুত্বের অনুপাত = ২৪.৩ : ১৮.৫ : ১

ইংরেজি বইয়ের দৈর্ঘ্য, প্রস্থ ও পুরুত্বের অনুপাত = ২৪.৩ : ১৮.৫ : ১

নিচের তথ্যগুলো দেখো এবং সেটির সাপেক্ষে অনুপাতগুলো নির্ণয় করো।

শ্রেণি	গড় বয়স
৩য়	৮
৫ম	১০
৭ম	১২

ক্রমিক	অনুপাত	অনুপাত	অনুপাতের সরল রুপ	পূর্ব রাশি	উত্তর রাশি
১	৩য় ও ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়স
২	৫ম ও ৭ম শ্রেণির শিক্ষার্থীদের গড় বয়স

সমাধানঃ

ক্রমিক	অনুপাত	অনুপাত	অনুপাতের সরল রুপ	পূর্ব রাশি	উত্তর রাশি
১	৩য় ও ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়স	৮:১০	৪:৫	৪	৫
২	৫ম ও ৭ম শ্রেণির শিক্ষার্থীদের গড় বয়স	১০:১২	৫:৬	৫	৬

কাজ:

১. উপরে ৩য়, ৫ম ও ৭ম শ্রেণির শিক্ষার্থীদের গড় বয়সের অনুপাতটি একত্রে কত হবে?

সমাধানঃ

৩য়, ৫ম ও ৭ম শ্রেণির শিক্ষার্থীদের গড় বয়সের অনুপাত

= ৮:১০:১২

= ৪:৫:৬

২. ৩য় ও ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়স যথাক্রমে ৭ ও ১০ বছর। অপরদিকে ৬ষ্ঠ শ্রেণির শিক্ষার্থীদের গড় বয়স ১১ বছর। এই তিন শ্রেণির শিক্ষার্থীদের গড় বয়স কি ধারাবাহিক অনুপাতে রয়েছে? থাকলে ধারাবাহিক অনুপাত আকারে অনুপাতটি কত হবে?

সমাধানঃ

প্রশ্নমতে,

৩য় ও ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়স যথাক্রমে ৭ ও ১০ বছর।

৫ম ও ৭ম শ্রেণির শিক্ষার্থীদের গড় বয়স যথাক্রমে ১০ ও ১১ বছর।

অর্থাৎ, এই তিন শ্রেণির শিক্ষার্থীদের গড় বয়স ধারাবাহিক অনুপাতে রয়েছে।

তাহলে, ধারাবাহিক অনুপাত আকারে অনুপাতটি হবেঃ ৭:১০:১১

একক কাজঃ

১. অনুপাত সংক্রান্ত নিচের ছকটি পূরণ করো:

সমাধানঃ এই প্রশ্নের সমাধান এই আর্টিকেলের প্রথমে দেয়া হয়েছে।

২. প্রথমেই তোমার বন্ধুর সাহায্যে বাম কাঁধ হতে বাম হাতের এবং ডান কাঁধ হতে ডান হাতের দৈর্ঘ্য মাপো। এবার তোমার নিজের উচ্চতা মাপো। তোমার প্রাপ্ত তথ্যগুলোর সাহায্যে নিচের ছক পূরণ করো।

বাম কাঁধ হতে বাম হাতের দৈর্ঘ্য (সেন্টিমিটারে)	ডান কাঁধ হতে ডান হাতের দৈর্ঘ্য (সেন্টিমিটারে)	পূর্ববর্তী দুটি কলামের যোগফল	তোমার উচ্চতা (সেন্টিমিটারে)	তোমার কাঁধ হতে দুই হাতের যোগফল এবং তোমার উচ্চতার অনুপাত

এখানে তুমি যে অনুপাতটি পেলে সেটি কোন ধরণের অনুপাত হল বলো তো?

সমাধানঃ

বাম কাঁধ হতে বাম হাতের দৈর্ঘ্য (সেন্টিমিটারে)	ডান কাঁধ হতে ডান হাতের দৈর্ঘ্য (সেন্টিমিটারে)	পূর্ববর্তী দুটি কলামের যোগফল	তোমার উচ্চতা (সেন্টিমিটারে)	তোমার কাঁধ হতে দুই হাতের যোগফল এবং তোমার উচ্চতার অনুপাত
৭৩ সেমি	৭৩ সেমি	১৪৬ সেমি	১৭০ সেমি	১৪৬:১৭০

এখন,

এখানে প্রাপ্ত অনুপাতটি একটি সরল ও লঘু অনুপাত।

বাস্তব সমস্যা সমাধানে অনুপাতের প্রয়োগঃ

অনুপাত সম্পর্কিত নিচের বাস্তব সমস্যাগুলি সমাধান করোঃ

১. পিতা ও পুত্রের বয়সের অনুপাত ১৪:৩। পিতার বয়স ৫৬ বছর হলে, পুত্রের বয়স কত?

সমাধানঃ

পিতা ও পুত্রের বয়সের অনুপাত ১৪:৩।

অতএব,

পুত্রের বয়স পিতার বয়সের ^৩/_১৪ অংশ।

এখন, পিতার বয়স  = ৫৬ বছর।

তাহলে,

পুত্রের বয়স = ৫৬ এর ^৩/_১৪ বছর

            = ৫৬×^৩/_১৪ বছর

            = ১২ বছর।

২. পায়েসে দুধ ও চিনির অনুপাত ৭: ২। ঐ পায়েসে চিনির পরিমাণ ৪ কেজি হলে, দুধের পরিমাণ কত ?

সমাধানঃ

পায়েসে দুধ ও চিনির অনুপাত ৭: ২

তাহলে,

পায়েসে দুধের পরিমান চিনির ^৭/_২ অংশ

= ৪×^৭/_২ কেজি [যেহেতু, পায়েসে চিনির পরিমাণ ৪ কেজি]

= ১৪ কেজি।

৩. দুইটি বইয়ের মূল্যের অনুপাত ৫:৭। দ্বিতীয়টির মূল্য ৮৪ টাকা হলে, প্রথমটির মূল্য কত?

সমাধানঃ

দুইটি বইয়ের মূল্যের অনুপাত ৫:৭

অতএব, ১ম বইয়ের মূল্য ২য় বইয়ের ^৫/_৭ অংশ

এখন, দ্বিতীয়টির মূল্য ৮৪ টাকা।

তাহলে,

২য় বইয়ের মূল্য

= ৮৪×^৫/_৭ টাকা

= ৬০ টাকা।

৪. দুইটি কম্পিউটারের দামের অনুপাত ৫: ৬। প্রথমটির দাম ২৫০০০ টাকা হলে, দ্বিতীয়টির দাম কত ? মূল্য বৃদ্ধির ফলে যদি প্রথমটির দাম ৫০০০ টাকা বেড়ে যায়, তখন তাদের দামের অনুপাতটি কী ধরনের অনুপাত ?

সমাধানঃ

দুইটি কম্পিউটারের দামের অনুপাত ৫: ৬

অতএব, দ্বিতীয়টির দাম প্রথমটির দামের ^৬/_৫ অংশ

এখন, প্রথমটির দাম ২৫০০০ টাকা

তাহলে,

দ্বিতীয়টির দাম

= ২৫০০০×^৬/_৫ টাকা

= ৫০০০×৬ টাকা

= ৩০০০০ টাকা।

আবার,

৫০০০ টাকা মূল্যবৃদ্ধিতে প্রথম কম্পিউটারের নতুন দাম = (৫০০০+২৫০০০) টাকা = ৩০০০০ টাকা।

সেক্ষেত্রে, দুইটি কম্পিউটারের দামের অনুপাত হবে ৩০০০০:৩০০০০ = ১:১।

তখন, তাদের দামের অনুপাতটি হলো একক অনুপাত।

৫. তিন বন্ধুর বাড়ি হতে স্কুলে আসা যাওয়ার সময়ের অনুপাত ২: ৩: ৪। ১ম বন্ধুর বাড়ি হতে স্কুলে যেতে ১৮ মিনিট লাগলে, বাকি দুই বন্ধুর বাড়ি হতে স্কুলে যেতে কত সময় লাগবে?

সমাধানঃ

তিন বন্ধুর বাড়ি হতে স্কুলে আসা যাওয়ার সময়ের অনুপাত ২: ৩: ৪।

অতএব,

২য় বন্ধুর বাড়ি হতে স্কুলে যেতে সময় লাগবে ১ম বন্ধুর সময়ের ^৩/_২ অংশ

= ১৮×^৩/_২ মিনিট [যেহেতু, ১ম বন্ধুর বাড়ি হতে স্কুলে যেতে ১৮ মিনিট লাগে]

= ২৭ মিনিট

এবং

৩য় বন্ধুর বাড়ি হতে স্কুলে যেতে সময় লাগবে ১ম বন্ধুর সময়ের ^৪/_২ অংশ

= ১৮×^৪/_২ মিনিট [যেহেতু, ১ম বন্ধুর বাড়ি হতে স্কুলে যেতে ১৮ মিনিট লাগে]

= ৩৬ মিনিট।

মিশ্র অনুপাত  – ৪র্থ অধ্যায় (৯১ – ৯৫ পৃষ্ঠা)

মিশ্র অনুপাত (Mixed Ratio)

একাধিক সরল অনুপাতের পূর্ব রাশিগুলোর গুলফল ও উত্তর রাশিগুলোর গুণফলকে যথাক্রমে পূর্ব ও উত্তর রাশি ধরে নতুন অনুপাত গঠন করলে তাকে মিশ্র অনুপাত (mixed ratio) বলে। যেমনঃ দুইটি সরল অনুপাত ৫:৩ ও ৬:৪ এর জন্য মিশ্র অনুপাতটি হবেঃ (৫×৬) : (৩×৪) = ৩০:১২।

কাজঃ উপরের পদ্ধতিতে দৈর্ঘ্য ও প্রস্থের অনুপাত ব্যবহার করে নিচের জমি দুইটির আকার বা ক্ষেত্রফলের তুলনা করো:

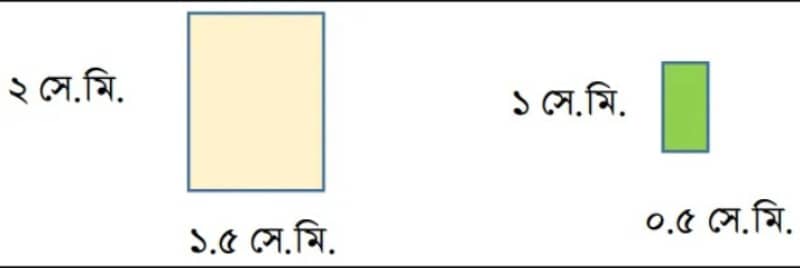
সমাধানঃ

জমি দুইটির দৈর্ঘ্যের অনুপাত = ^২/_১ = ২ : ১

জমি দুইটির প্রস্থের অনুপাত = ^১.৫/_০.৫ = ১.৫ : ০.৫

এখন,

জমি দুইটির দৈর্ঘ্য ও প্রস্থের অনুপাতের গুনফল

= ^২/_১×^১.৫/_০.৫

= ^৩/_০.৫

= ^৬/_১

= ৬ : ১

অর্থাৎ, প্রথম জমিটির আকার বা ক্ষেত্রফল দ্বিতীয় জমির থেকে ৬ গুণ বড়।

শিখনঃ দুইটি আয়তাকার মাঠের দৈর্ঘ্যের অনুপাত ৪:৩ এবং প্রস্থের অনুপাত ৬:১। মাঠের ক্ষেত্রফলের অনুপাত কত হবে?

সমাধানঃ

১ম আয়তাকার মাঠের দৈর্ঘ্যের অনুপাত = ^৪/_৩

২য় আয়তাকার মাঠের দৈর্ঘ্যের অনুপাত = ^৬/_১

এখন,

দুইটি অনুপাতের গুণফল

= ^৪/_৩×^৬/_১

= ^২৪/_৩

= ^৮/_১

= ৮ : ১

তাহলে, মাঠ দুইটির ক্ষেত্রফলের অনুপাত = ৮ : ১।

শিখনঃ পৃষ্ঠা ৯৩

১) ২ : ৩ ও ৩ : ৪ অনুপাতদ্বয়ের মিশ্র অনুপাত নির্ণয় করো।

সমাধানঃ

অনুপাতদ্বয়ের পূর্ব রাশিগুলোর গুণফল = ২×৩ = ৬

এবং উত্তর রাশিগুলোর গুণফল = ৩×৪ = ১২

অতএব, নির্ণেয় মিশ্র অনুপাত = ৬ : ১২ = ১ : ২।

২) নিচের সরল অনুপাতগুলোকে মিশ্র অনুপাতে প্রকাশ কর :

(ক) ৩:৫, ৫:৭ ও ৭:৯

(খ) ৫:৩, ৭:৫ ও ৯:৭

সমাধানঃ

(ক) ৩:৫, ৫:৭ ও ৭:৯

অনুপাত তিনটির পূর্ব রাশিগুলোর গুণফল = ৩×৫×৭ = ১০৫

এবং উত্তর রাশিগুলোর গুণফল = ৫×৭×৯ = ৩১৫

তাহলে,

নির্ণেয় মিশ্র অনুপাত = ১০৫:৩১৫ = ১:৩।

(খ) ৫:৩, ৭:৫ ও ৯:৭

অনুপাত তিনটির পূর্ব রাশিগুলোর গুণফল = ৫×৭×৯ = ৩১৫

এবং উত্তর রাশিগুলোর গুণফল = ৩×৫×৭ = ১০৫

তাহলে,

নির্ণেয় মিশ্র অনুপাত = ৩১৫:১০৫ = ৩:১।

৩) ত্রিমাত্রিক বস্তুর ক্ষেত্রে তুলনা করার সময় দৈর্ঘ্য, প্রস্থ ও উচ্চতা তিনটিই বিবেচনা করতে হয়।

অর্থাৎ, আয়তনের মাধ্যমে ত্রিমাত্রিক বস্তুর তুলনা সুবিধাজনক হয়।

এবার ভেবে দেখতো আয়তন নির্ণয় না করেও অন্য কোন উপায়ে নিচের ছবির আয়তাকার ঘনবস্তু দুটির আয়তনের অনুপাত নির্ণয় করতে পারো কিনা?

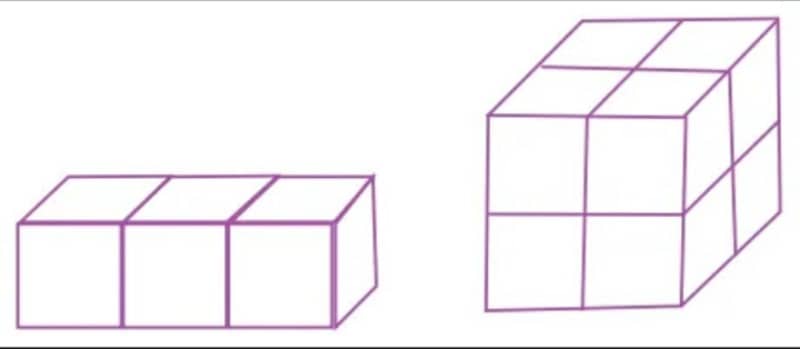
সমাধানঃ

মনে করি, আয়তাকার ঘনবস্তু দুইটির ক্ষুদ্রতম ঘনকের দৈর্ঘ্য = ১ একক।

তাহলে,

১ম আয়তাকার ঘনবস্তুর দৈর্ঘ্য = ৩ একক, প্রস্থ = ১ একক ও উচ্চতা = ১ একক।

২য় আয়তাকার ঘনবস্তুর দৈর্ঘ্য = ২ একক, প্রস্থ = ২ একক ও উচ্চতা = ২ একক।

অতএব,

ঘনবস্তু দুইটির দৈর্ঘ্যের অনুপাত = ৩ : ২

ঘনবস্তু দুইটির প্রস্থের অনুপাত = ১ : ২

ঘনবস্তু দুইটির উচ্চতার অনুপাত = ১ : ২

এখন,

অনুপাত তিনটির পূর্ব রাশিরগুলোর গুণফল = ৩×১×১ = ৩

এবং উত্তর রাশিগুলোর গুণফল = ২×২×২ = ৮

অর্থাৎ, মিশ্র অনুপাত = ৩ : ৮

সুতরাং, আয়তাকার ঘনবস্তু দুইটির আয়তনের অনুপাত = ৩ : ৮।

অনুপাত ও শতকরা

একক কাজ: একটি স্কুলে শিক্ষার্থীর সংখ্যা ৮০০ জন। বছরের শুরুতে ৫% শিক্ষার্থী নতুন ভর্তি করা হলে, বর্তমানে ঐ স্কুলে শিক্ষার্থীর সংখ্যা কত?

সমাধানঃ

স্কুলটিতে শিক্ষার্থীর সংখ্যা = ৮০০ জন।

তাহলে,

নতুন শিক্ষার্থীর সংখ্যা

= ৮০০ এর ৫%

= ৮০০×৫%

= ৮০০×^৫/_১০০

= ৪০ জন।

সুতরাং, বর্তমানে ঐ স্কুলে শিক্ষার্থীর সংখ্যা = ৮০০ + ৪০ জন = ৮৪০ জন।

সমস্যা:

কলার দাম ১৪^২/_৭% কমে যাওয়ায় ৪২০ টাকায় পূর্বাপেক্ষা ১০ টি কলা বেশি পাওয়া যায়।

(ক) একটি সংখ্যার ১৪^২/_৭% = ১০ হলে, সংখ্যাটি নির্ণয় করো।

(খ) প্রতি ডজন কলার বর্তমান দাম কত?

(গ) প্রতি ডজন কলা কত দামে বিক্রয় করলে ৩৩% লাভ হতো।

সমাধানঃ

(ক)

মনে করি, সংখ্যাটি a

প্রশ্নমতে,

a×১৪^২/_৭% = ১০

বা, a×(^১০০/_৭)% = ১০

      a×১০০

বা, ———- = ১০

      ৭×১০০

বা, ^a/_৭ = ১০

বা, a = ১০×৭

বা, a = ৭০

অতএব, নির্ণেয় সংখ্যাটি ৭০।

(খ)

ধরি,

পূর্বে ৪২০ টাকায় পাওয়া যেত a টি কলা

অর্থাৎ, পূর্বে ১টি কলার দাম ছিল ^৪২০/_a টাকা।

আবার,

বর্তমানে ৪২০ টাকায় পাওয়া যায় a+১০ টি কলা।

অর্থাৎ, বর্তমানে ১টি কলার দাম = ^৪২০/_(a+১০) টাকা

তাহলে,

কলার পূর্বের ও বর্তমান দামের অনুপাত

= ^৪২০/_a : ^৪২০/_(a+১০)

= ^১/_a : ^১/_(a+১০) …….(i)

এখন,

১৪^২/_৭% দাম কমার অর্থ,

কলার পূর্বের দাম ১০০ টাকা হলে বর্তমান দাম

= (১০০-১৪^২/_৭) টাকা

= ১০০ – ^১০০/_৭ টাকা

    ৭০০ – ১০০

= ————– টাকা

            ৭

= ^৬০০/_৭ টাকা

তাহলে,

কলার পূর্বের ও বর্তমান দামের অনুপাত

= ১০০ : ^৬০০/_৭

= ৭০০ : ৬০০

= ৭ : ৬  …….. (ii)

এখন (i) ও (ii) হতে পাই,

^১/_a : ^১/_(a+১০) = ৭ : ৬ 

           ^১/_a

বা, ———- = ^৭/_৬

          ^১/_(a+১০)

      a+১০

বা, ———- = ^৭/_৬

         a

বা, ৬(a+১০) = ৭a

বা, ৬a + ৬০ = ৭a

বা, ৬a-৭a = – ৬০

বা, -a = -৬০

বা, a = ৬০

সুতরাং, আমরা পাই পূর্বে ৪২০ টাকায় ৬০টি কলা পাওয়া যেত।

তাহলে, বর্তমানে ৪২০ টাকায় কলা পাওয়া যায় ৬০+১০ টি = ৭০ টি।

অতএব,

বর্তমানে, ১টি কলার দাম = ^৪২০/_৭০ টাকা = ৬ টাকা

তাহলে, বর্তমানে এক ডজন বা ১২ টি কলার দাম = ৬×১২ = ৭২ টাকা।

(গ)

৩৩% লাভে ক্রয়মূল্য ১০০ টাকা হলে বিক্রয়মূল্য = (১০০+৩৩) টাকা = ১৩৩ টাকা।

অর্থাৎ, ক্রয়মূল্য ও বিক্রয় মূল্যের অনুপাত = ১০০ : ১৩৩ …… (iii)

এখন, ক হতে পাই,

বর্তমানে ১টি কলার ক্রয়মূল্য = ৬ টাকা।

ধরি, ৩৩% লাভে ১টি কলা b টাকায় বিক্রি করা হলো, তখন ক্রয়মূল্য ও বিক্রয় মূল্যের অনুপাত

= ৬ : b ….. (iv)

এখন, (iii) ও (iv) হতে পাই,

১০০ : ১৩৩ = ৬ : b

বা, ^১০০/_১৩৩ = ^৬/_b

বা, ১৩৩×৬ = ১০০×b

বা, ১০০b = ৭৯৮

বা, b = ^৭৯৮/_১০০

অর্থাৎ, ১টি কলার বিক্রয়মূল্য = ^৭৯৮/_১০০ টাকা

তাহলে, ১২টি বা এক ডজন কলার বিক্রয়মূল্য = (^৭৯৮/_১০০)×১২টাকা = ^{৭৯৮×৩}/_২৫ টাকা = ^২৩৯৪/_২৫ টাকা =৯৫^১৯/_২৫ টাকা।

সমানুপাত ও ক্রমিক সমানুপাত – ৪র্থ অধ্যায় (১০৪ – ১০৬ পৃষ্ঠা)

সমানুপাত ও ক্রমিক সমানুপাত

দুই বা ততোধিক অনুপাত সমান হলে সেই সকল সমান অনুপাতকে পরস্পরের সাপেক্ষে সমানুপাত বলা হয়। যেমনঃ ১:২ = ৩:৬ মানে এরা পরস্পর সমানুপাত। আবার, যে সমানুপাতে, অনুপাতের মধ্যপদ দুটি সমান হয়, সেই সমানুপাতটিকে ক্রমিক সমানুপাত বলা হয়। যেমনঃ ১:২ ও ২:৪ এর বেলায় মধ্যপদ ২ একই অর্থাৎ এরা ক্রমিক সমানুপাত।

কাজ: ১০৫ নং পৃষ্ঠায় প্রদত্ত সমস্যাবলি।

১) ছকে ৪র্থ ঘণ্টা শেষে বাসটির অতিক্রান্ত দুরত্ব নির্ণয় করো।

সমাধানঃ

পাঠ্যবইয়ে সময়ের সাথে একটি বাসের অতিক্রান্ত দূরত্বের ছকটি নিন্মরুপঃ

সময় (ঘন্টায়)	১	২	৩	৪	৫
দুরত্ব (কিলোমিটারে)	৫০		১৫০		২৫০

এবং বলা আছে যে প্রতি ঘণ্টায় বাসটির অতিক্রান্ত দুরত্ব, সময়ের সাপেক্ষে সমানুপাতিক।

সুতরাং শর্ত অনুসারে ৪র্থ ঘন্টা শেষে বাসটির অতিক্রান্ত দুরত্ব ক কিলোমিটার হলে,

১ : ৫০ = ৪ : ক

বা, ^১/_৫০ = ^৪/_ক

বা, ক = ৫০×৪

বা, ক = ২০০

অতএব, ৪র্থ ঘন্টা শেষে বাসটির অতিক্রান্ত দুরত্ব ২০০ কিলোমিটার।

২) কোন সমানুপাতের ১ম, ২য় ও ৪র্থ রাশি যথাক্রমে ৯, ১৮ ও ২০ হলে ৩য় রাশিটি কত হবে?

সমাধানঃ

সমানুপাতের সংজ্ঞা অনুসারে,

১ম-রাশি : ২য়-রাশি = ৩য়-রাশি : ৪র্থ-রাশি

বা, ৯ : ১৮ = ৩য় রাশি : ২০

বা, ^৯/_১৮ = ^{৩য় রাশি}/_২০

বা, ৩য় রাশি×১৮ = ২০×৯

বা, ৩য় রাশি = ^২০×৯/_১৮

বা, ৩য় রাশি = ১০

অতএব, ৩য় রাশিটি হবে ১০।

৩) রানার কাছে ৪ টি পেন্সিল এবং ৫ টি কলম রয়েছে। অপরদিকে সজীবের কাছে ১০ টি কলম রয়েছে। এখন যদি রানা ও সজীবের পেন্সিল কলমের অনুপাত সমানুপাত হয়, তাহলে সজিবের কাছে কতটি পেন্সিল রয়েছে?

সমাধানঃ

রানার কাছে পেন্সিল ও কলম রয়েছে যথাক্রমে ৪টি ও ৫টি।

অর্থাৎ, রানার কাছে থাকা পেন্সিল ও কলমের অনুপাত = ৪ : ৫

আবার,

সজীবের কাছে কলম আছে ১০টি।

এখন,

মনে করি, সজীবের কাছে পেন্সিল আছে ক টি

তাহলে,

সজীবের কাছে পেন্সিল ও কলমের অনুপাত = ক : ১০

শর্ত অনুসারে,

৪ : ৫ = ক : ১০

বা, ^৪/_৫ = ^ক/_১০

বা, ৫ক = ৪×১০

বা, ৫ক = ৪০

বা, ক = ^৪০/_৫

বা, ক = ৮

অতএব, সজীবের কাছে পেন্সিল আছে ৮ টি।

৪) ২০ কিলোমিটার দীর্ঘ একটি গাড়ির রেসে কয়েকটি গাড়ি অংশগ্রহণ করে। এর মধ্যে যে গাড়িটি রেসে বিজয়ী হয় সেই গাড়ির ১০ মিনিট পর্যন্ত নির্দিষ্ট সময় ব্যবধানে অতিক্রান্ত দুরত্বের তথ্য দেয়া রয়েছে। এখানে মজার ব্যাপার হল, সেই গাড়িটি সবসময় একই গতি ধরে দুরত্ব অতিক্রম করেছে। এখন তুমি নিচের আংশিক পূর্ণ ছকটি দেখো এবং সমানুপাতের ধারণা ব্যবহার করে সম্পূর্ণ করো।

সময় (মিনিট)	১	২	৩	৪	৫	৬		৮		১০
অতিক্রান্ত দুরত্ব (কিলোমিটার)	২	৪				১২	১৪	১৬	১৮

সমাধানঃ

মনে করি, ৩ মিনিট পর গাড়িটির অতিক্রান্ত দূরত্ব = ক কিমি।

তাহলে,

১ : ২ = ৩ : ক

বা, ^১/_২ = ^৩/_ক

বা, ক = ৬

সমানুপাতের এই নিয়ম অনুসারে প্রদত্ত ছকটি পূরণ করে পাই,

সময় (মিনিট)	১	২	৩	৪	৫	৬	৭	৮	৯	১০
অতিক্রান্ত দুরত্ব (কিলোমিটার)	২	৪	৬	৮	১০	১২	১৪	১৬	১৮	২০

একক কাজ:

একটি ক্রমিক সমানুপাতের ১ম ও ৩য় রাশি যথাক্রমে ৪ ও ১৬ হলে, মধ্য সমানুপাতী ও ক্রমিক সমানুপাত নির্ণয় করো।

সমাধানঃ

আমরা জানি,

৩টি রাশি ক্রমিক সমানুপাতী হলে,

১ম রাশি×৩য় রাশি = (২য় রাশি)^২

বা, (২য় রাশি)^২ = ৪×১৬

বা, (২য় রাশি)^২ = ৬৪

বা, ২য় রাশি = √৬৪

বা, ২য় রাশি = ৮

তাহলে, নির্ণেয় মধ্য সমানুপাতী = ৮

এবং ক্রমিক সমানুপাত = ৪ : ৮ :: ৮ : ১৬

পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

👉 আকৃতি দিয়ে যায় চেনা – ৫ম অধ্যায় – সমাধান | গণিত | সপ্তম শ্রেণী | Class 7 Math Chapter 5 | BD 2023