সূচকের সূচক (২২- ৩২ পৃষ্ঠা)  – সমাধান | ১ম অধ্যায় | গণিত | সপ্তম শ্রেণী | Class 7 | Math | Chapter 1 (22-32 page)

এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর প্রথম অধ্যায় সূচকের গল্প (২২ – ৩২ পৃষ্ঠা), সূচকের সূচক সম্পর্কে।

সূচকের সূচক

শিখনঃ বিদ্যালয়ে তোমাকে ১ম দিন ১টি ক্যান্ডি দেওয়া হলো এবং বাকী দিনগুলোতে পূর্বের দিনে প্রাপ্ত ক্যান্ডির সাথে তোমার রোল নাম্বারের শেষ অঙ্কের গুণফলের সমান ক্যান্ডি দেয়া হলো। মোট ৫ দিনের ক্যান্ডি প্রাপ্তির সংখ্যার ছক নির্ণয় কর যেখানে তোমার রোল নাম্বার ২৬। (ছকে অবশ্যই গুণফলের সূচক আকারে প্রকাশ করতে হবে। কোন ক্ষেত্রেই তোমাদের গুণফলটিকে প্রকাশ করতে হবে না)

সমাধানঃ

ছক – ৫.১

রোল	রোলের শেষ অঙ্ক	দিন	প্রাপ্ত ক্যান্ডি সংখ্যা
২৬	৬	১ম	১ = ৬০
		২য়	১×৬ = ৬১
		৩য়	১×৬×৬ = ৬২
		৪র্থ	১×৬×৬×৬ = ৬৩
		৫ম	১×৬×৬×৬×৬ = ৬৪

শিখনঃ ছক ৫.২ পূরণ করো। শর্তঃ তোমাদের দলে ৫ জন শিক্ষার্থী আছে যাদের রোলের শেষ অংক তোমার রোলের শেষ অঙ্কের সমান এবং বাকী শর্ত পূর্বের অনুরুপ।

সমাধানঃ

ছক – ৫.২

রোল	রোলেরশেষঅংক	দিন	১ম জনেরপ্রাপ্তক্যান্ডিসংখ্যা	১ম জনেরপ্রাপ্ত ক্যান্ডিসংখ্যারগুণাকার	দলের সকলের প্রাপ্ত ক্যান্ডি সংখ্যার গুণাকার	সূচকীয় আকারে গুণফল
২৬	৬	১ম	১	১	৬০×৬০×৬০×৬০×৬০	৬০
		২য়	৬	৬	৬১×৬১×৬১×৬১×৬১	৬৫
		৩য়	৬২	৬×৬	৬২×৬২×৬২×৬২×৬২	৬৮
		৪র্থ	৬৩	৬×৬×৬	৬৩×৬৩×৬৩×৬৩×৬৩	৬১৫
		৫ম	৬৪	৬×৬×৬×৬	৬৪×৬৪×৬৪×৬৪×৬৪	৬২০

শিখনঃ দলে ৫ জন সদস্য ও প্রত্যেকে ১০ এর গুণীতক হারে ক্যান্ডি পায়, তবে ছক ৫.৩ পূরণ করো।

সমাধানঃ

ছক – ৫.৩

দিন	১মজনেরপ্রাপ্তক্যান্ডিসংখ্যা	১ম জনের প্রাপ্তক্যান্ডি সংখ্যারগুণাকার	দলের সকলের প্রাপ্ত ক্যান্ডিসংখ্যার গুণাকার	সূচকের গূনের নিয়মব্যবহার করে,সূচকীয় আকারে গুণফল
১ম	১০০	১	১০০×১০০×১০০×১০০×১০০	১০০+০+০+০+০= ১০০
২য়	১০১	১০	১০১×১০১×১০১×১০১×১০১	১০১+১+১+১+১= ১০৫
৩য়	১০২	১০×১০	১০২×১০২×১০২×১০২×১০২	১০২+২+২+২+২= ১০১০
৪র্থ	১০৩	১০×১০×১০	১০৩×১০৩×১০৩×১০৩×১০৩	১০৩+৩+৩+৩+৩= ১০১৫
৫ম	১০৪	১০×১০×১০×১০	১০৪×১০৪×১০৪×১০৪×১০৪	১০৪+৪+৪+৪+৪= ১০২০

শিখনঃ

১০×১০ = ১০^২

আবার,

১০^৩×১০^৩ = (১০^৩)^২ = ১০^৬

এই নিয়মে পাঠ্যবইয়ের ছক ৫.৪ পূরণ করো।

সমাধানঃ

ছক ৫.৪

গুণ-আকার	সূচকীয় আকার
১০×১০×১০×১০×১০	১০৫
১০২×১০২×১০২×১০২×১০২	(১০২)৫ = ১০১০
১৪×১৪×১৪×১৪×১৪×১৪×১৪	১৪৭
১৪৩×১৪৩×১৪৩×১৪৩×১৪৩×১৪৩×১৪৩	(১৪৩)৭ = ১৪২১

শিখনঃ ৫.৫ এর ফাঁকা ঘরগুলো বা আংশিক পূর্ণ ঘরগুলো সম্পূর্ণ করো।

সমাধানঃ

ছক – ৫.৫

দিন	১ম জনেরপ্রাপ্ত ক্যান্ডিসংখ্যা	১ম জনের প্রাপ্তক্যান্ডি সংখ্যারগুণাকার	দলের সকলের প্রাপ্ত ক্যান্ডি সংখ্যার গুণাকার	সূচকের সূচকীয় আকারে গুণফল
১ম	১০০	১	১×১×১×১×১	(১০০)৫
২য়	১০১	১০	১০১×১০১×১০১×১০১×১০১	(১০১)৫
৩য়	১০২	১০×১০	১০২×১০২×১০২×১০২×১০২	(১০২)৫
৪র্থ	১০৩	১০×১০×১০	১০৩×১০৩×১০৩×১০৩×১০৩	(১০৩)৫
৫ম	১০৪	১০×১০×১০×১০	১০৪×১০৪×১০৪×১০৪×১০৪	(১০৪)৫

শিখনঃ সূচকের সূচকীয় আকারে গুণফল প্রকাশের পদ্ধতি অনুসারে ছক ৫.৬ পূরণ করো।

সমাধানঃ

ছক – ৫.৬

রোল	রোলেরশেষঅংক	দিন	১ম জনেরপ্রাপ্তক্যান্ডিসংখ্যা	১ম জনেরপ্রাপ্ত ক্যান্ডিসংখ্যারগুণাকার	দলের সকলের প্রাপ্ত ক্যান্ডি সংখ্যার গুণাকার	সূচকীয় আকারে গুণফল
২৬	৬	১ম	১	১	৬০×৬০×৬০×৬০×৬০	(৬০)৫
		২য়	৬০	৬	৬১×৬১×৬১×৬১×৬১	(৬১)৫
		৩য়	৬২	৬×৬	৬২×৬২×৬২×৬২×৬২	(৬২)৫
		৪র্থ	৬৩	৬×৬×৬	৬৩×৬৩×৬৩×৬৩×৬৩	(৬৩)৫
		৫ম	৬৪	৬×৬×৬×৬	৬৪×৬৪×৬৪×৬৪×৬৪	(৬৪)৫

শিখনঃ ৫.২ ও ৫.৫ ছক হতে প্রাপ্ত তথ্যের শায্যে ৫.৭ ছকটি পূরণ করো।

সমাধানঃ

ছক – ৫.৭

দলের সকলের প্রাপ্ত ক্যান্ডি সংখ্যার গুণাকার	সূচকের সূচকীয় আকারে গুণফল	সূচকের গুণের নিয়ম ব্যবহার করে, সূচকীয় আকারে গুণফল
১×১×১×১×১	(১০০)৫	১০০ = ১
১০×১০×১০×১০×১০	(১০১)৫	১০৫
১০২×১০২×১০২×১০২×১০২	(১০২)৫	১০১০
১০৩×১০৩×১০৪×১০৪×১০৪	(১০৩)৫	১০১৫
১০৪×১০৪×১০৪×১০৪×১০৪	(১০৪)৫	১০২০

শিখনঃ ছক ৫.৩ ও ৫.৬ এর তথ্য মোতাবেক ৫.৮ ছকটি পূরন করো।

সমাধানঃ

 ছক – ৫.৮

দলের সকলের প্রাপ্ত ক্যান্ডি সংখ্যার গুণাকার	সূচকের সূচকীয় আকারে গুণফল	সূচকের গুণের নিয়ম ব্যবহার করে, সূচকীয় আকারে গুণফল
১×১×১×১×১	(৬০)৫	৬০ = ১
৬×৬×৬×৬×৬	(৬১)৫	৬৫
৬২×৬২×৬২×৬২×৬২	(৬২)৫	৬১০
৬৩×৬৩×৬৪×৬৪×৬৪	(৬৩)৫	৬১৫
৬৪×৬৪×৬৪×৬৪×৬৪	(৬৪)৫	৬২০

শিখন ফলাফলঃ

১০^২ × ১০^২ × ১০^২ × ১০^২ × ১০^২ কে লেখা যায় (১০^২)^৫ হিসেবে এবং (১০^২)^৫ কে লেখা যায়, ১০^২×৫ =১০^১০ হিসেবে।

কাজঃ

১) নিচের সূচকগুলো নির্ণয় করো বা নিচের সূচকগুলোকে সূচকের সূচক আকারে প্রকাশ করো।

১. ৮^১৪×৮^১৪×৮^১৪×৮^১৪

২. ৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২

৩. ১৪^৩×১৪^৩

৪. ১৮^৯×১৮^৯×১৮^৯×১৮^৯

৫. ২৫^৪

সমাধানঃ

১. ৮^১৪×৮^১৪×৮^১৪×৮^১৪ = (৮^১৪)^৪

২. ৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২×৬^২ = (৬^২)^১১

৩. ১৪^৩×১৪^৩ = (১৪^৩)^২

৪. ১৮^৯×১৮^৯×১৮^৯×১৮^৯ = (১৮^৯)^৪

৫. ২৫^৪ = (২৫^৪)^১

২) নিচের সূচকের সংক্ষিপ্ত আকার গুলো নির্ণয় করো।

১. (৪৩^৭)^১১

২. (৯৯^২)^৪

৩. (৩৪^৩)^৭

৪. (২^-২)^৩

৫. (১৩^৩)^১

সমাধানঃ

১. (৪৩^৭)^১১ = ৪৩^৭×^১১ = ৪৩^৭৭

২. (৯৯^২)^৪ = ৯৯^২×৪ = ৯৯^৮

৩. (৩৪^৩)^৭ = ৩৪^৩×৭ = ৩৪^২১

৪. (২^-২)^৩ = ২^-২×৩ = ২^-৬

৫. (১৩^৩)^১ = ১৩^৩×১ = ১৩^৩

একক কাজঃ

ছবির বাবা তার ব্যাংকের ক্রেডিট কার্ডের পিন ভুলে গেছেন। তখন ছবির মনে পড়লো নিচের চিত্রের সাহায্যে পিনটি খজেুঁ পাওয়া সম্ভব। তোমরা কি ছবিকে সাহায্য করতে পারবে?

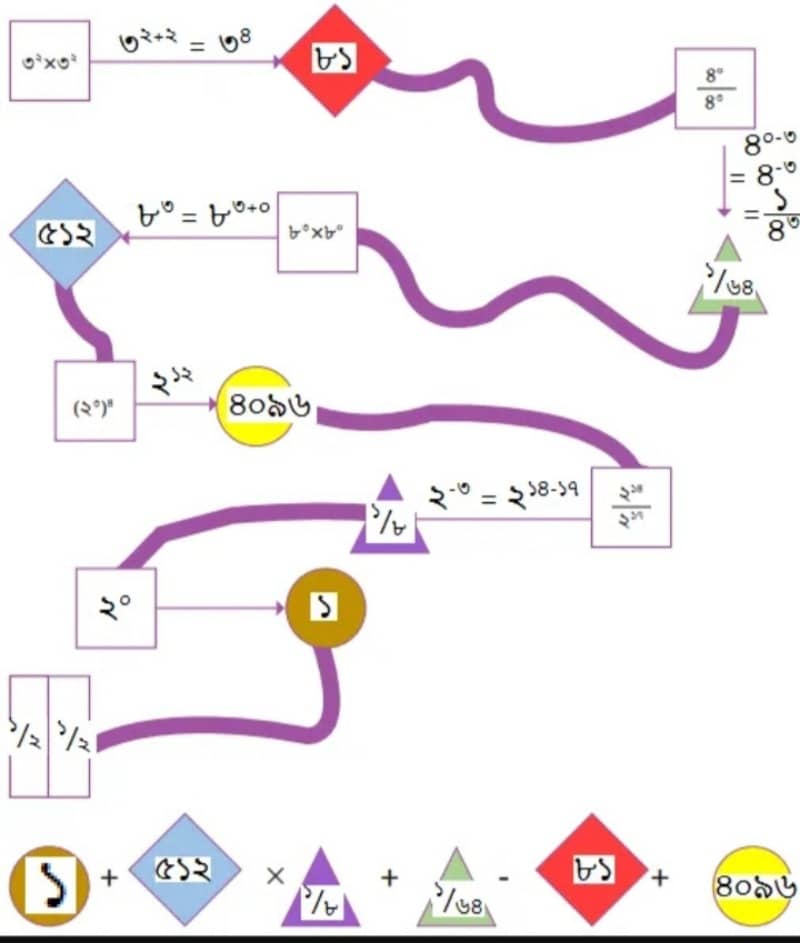
সমাধানঃ

প্রদত্ত হিসাবগুলি সমাধান করে চিত্রে প্রদত্ত রঙ্গিন ক্ষেত্রগুলোর মান বের করে সরল অংশে মানগুলো বসিয়ে পাই,

১ + ৫১২ × ^১/_৮ + ^১/_৬৪ – ৮১ + ৪০৯৬

= ১ + ৬৪ + ^১/_৬৪ – ৮১ + ৪০৯৬

= ৪০৮০ + ^১/_৬৪

= ৪০৮০ + ০.১৫৬২৫

অর্থাৎ, পিনটি হবে ৪০৮০ [কারন পিন ভগ্নাংশ হবে না]

👉 সূচকের ভাগ (১৪-২২ পৃষ্ঠা)  – সমাধান | ১ম অধ্যায় | গণিত | সপ্তম শ্রেণী 

আরও একটু সূচক

শিখনঃ

সূর্য থেকে পৃথিবীতে আলো এসে পৌঁছাতে সময় লাগে ৮ মিনিট ১৮ সেকেন্ড।

সূর্য থেকে পৃথিবীর দুরত্ব ১৫,০০,০০,০০০ কিলোমিটার।

আলোর গতিবেগ প্রতি সেকেন্ডে ৩০,০০,০০,০০০ মিটার

কাজঃ

১) পৃথিবী থেকে সূর্যের দুরত্ব কথায় কত হবে চিন্তা করে বলো তো।

উত্তরঃ পনের কোটি কিলোমিটার।

২) আলোর বেগ কথায় কত হবে চিন্তা করে বলো তো।

উত্তরঃ ত্রিশ কোটি মিটার।

শিখনঃ আলোর গতিবেগকে সূচকের মাধ্যমে প্রকাশ করো। পাঠ্যবইয়ের ছক ৭.১ অনুসারে।

সমাধানঃ

ছক – ৭.১

সংখ্যা (আলোর বেগ)	১০ দ্বারা ভাগ করে প্রকাশ	সূচক আকারে প্রকাশ
৩০০০০০০০০	৩০০০০০০০×১০	৩০০০০০০০×১০
	৩০০০০০০×১০×১০	৩০০০০০০×১০২
	৩০০০০০×১০×১০×১০	৩০০০০০×১০৩
	৩০০০০×১০×১০×১০×১০	৩০০০০×১০৪
	৩০০০×১০×১০×১০×১০×১০	৩০০০×১০৫
	৩০০×১০×১০×১০×১০×১০×১০	৩০০×১০৬
	৩০×১০×১০×১০×১০×১০×১০×১০	৩০×১০৭
	৩×১০×১০×১০×১০×১০×১০×১০×১০	৩×১০৮

শিখনঃ পৃথিবী থেকে সূর্যের দূরত্বকে সূচকের মাধ্যমে ছক ৭.১ এর ন্যায় প্রকাশ করো।

সমাধানঃ

ছক – ৭.২

সংখ্যা (পৃথিবী থেকে সূর্যের দুরত্ব	১০ দ্বারা ভাগ করে প্রকাশ	সূচক আকারে প্রকাশ
১৫০০০০০০০	১৫০০০০০০×১০	১৫০০০০০০×১০
	১৫০০০০০×১০×১০	১৫০০০০০×১০২
	১৫০০০০×১০×১০×১০	১৫০০০০×১০৩
	১৫০০০×১০×১০×১০×১০	১৫০০০×১০৪
	১৫০০×১০×১০×১০×১০×১০	১৫০০×১০৫
	১৫০×১০×১০×১০×১০×১০×১০	১৫০×১০৬
	১৫×১০×১০×১০×১০×১০×১০×১০	১৫×১০৭

শিখনঃ ১৫×১০^৭ সংখ্যাটিতে ১৫ কে ১০ থেকে ছোট সংখ্যার মাধ্যমে লিখে সংখ্যাটিকে প্রকাশ করো।

সমাধানঃ

১৫×১০^৭ = ১.৫×১০^৮  [এখানে ১.৫ < ১০]

শিখন ফলাফলঃ

১. ১ হাজার কে সূচকের সাহায্যে লিখ।

উত্তরঃ ১×১০^৩

২. বাস্তবের বিভিন্ন বড় সংখ্যাকে সূচকের মাধ্যমে ছোট আকারে প্রকাশ করা যায়। প্রকাশের উপায় নিয়ে, উপরের দুটি উদাহরণ থেকে তোমার অনুধাবন নিচের প্রশ্নের উত্তরের সাহায্যে প্রকাশ করো।

(ক) ভাগের কাজটি কখন শেষ করব?

(খ) ভাগ করে সূচক বিহীন যে সংখ্যাটি পাবো, তা কি ১ এর চেয়ে ছোট হতে পারবে? কিংবা ১ এর সমান হতে পারবে?

(গ) ভাগ করে সূচক বিহীন যে সংখ্যাটি পাবো, তা কি ১০ এর সমান কিংবা বড় হতে পারবে?

উত্তরঃ

(ক) সূচক বিহীন সংখ্যাটি ১ এর সমান অথবা ১ এর চেয়ে বড় কিন্তু ১০ এর চেয়ে ছোট হলেই ভাগের কাজটি শেষ করব।

(খ) ভাগ করে সূচক বিহীন যে সংখ্যাটি পাবো তা ১ এর চেয়ে ছোট হতে পারবে না কিন্তু ১ এর সমান হতে পারবে।

(গ) ভাগ করে সূচক বিহীন যে সংখ্যাটি পাবো তা ১০ এর সমান বা ১০ এর চেয়ে বড় হতে পারবে না।

কাজ: পৃথিবী থেকে চাঁদের দুরত্ব প্রায় ৩,৮৪,০০০ কিলোমিটার। এই দুরত্বকে গাণিতিক ভাষায় ছোট আকারে প্রকাশ করো।

সমাধানঃ

৩৮৪০০০

= ৩৮৪০০×১০^১

= ৩৮৪০×১০^২

=৩৮৪×১০^৩

= ৩৮.৪×১০^৪

= ৩.৮৪×১০^৫

অতএব, ৩,৮৪,০০০ কিলোমিটার এর গাণিতিক ভাষায় ছোট আকার হলোঃ ৩.৮৪×১০^৫ কিলমিটার।

একক কাজঃ

একক কাজঃ

১) তোমরা নিশ্চয় কোভিড-১৯ মহামারী সম্পর্কে অবগত আছো। মারাত্মক ছোঁয়াচে এই মহামারীর কারণে পুরো পৃথিবী একটা বড় সময় স্থবির হয়ে ছিল। আমরা সেই মহামারী নিয়ে একটি গণনা করার চেষ্টা করব। ধরো, একটি বাড়িতে ৩ জন লোক আছে। তারা প্রত্যেকেই কোভিড আক্রান্ত হয়েছে। এখন হিসাব করে দেখা গেল, তাঁরা ৩ জন প্রত্যেকেই ১ দিনে আলাদা-আলাদাভাবে ন্যুনতম ৩ জনকে আক্রান্ত করতে সক্ষম। আবার তাঁদের দ্বারা আক্রান্ত প্রত্যেকে আবার এক দিনে আলাদা-আলাদাভাবে ন্যুনতম ৩ জন করে ব্যাক্তিকে আক্রান্ত করতে সক্ষম।

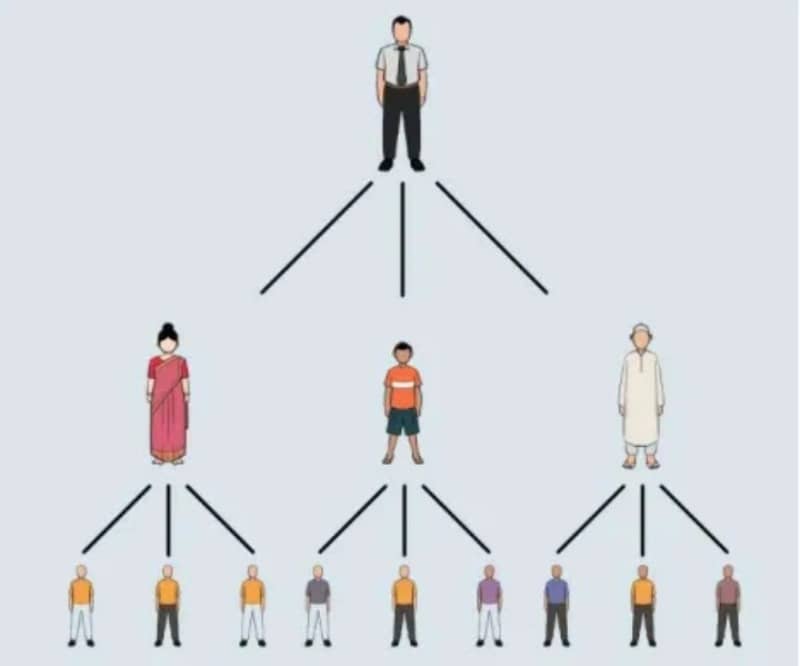
সূচকের ধারণার সাপেক্ষে বলো তো কোনরকম স্বাস্থ্যবিধি মানা না হলে, পরবর্তী ৫ দিনে সর্বনিন্ম কতজন কোভিড-১৯ আক্রান্ত ব্যাক্তি থাকতে পারবে? ছক অনুযায়ী পূরণ করার চেষ্টা করো। এই ধারায় ১১তম ও ১৪তম দিন শেষে সর্বনিন্ম কতজন আক্রান্ত রোগী থাকা সম্ভব?

সমাধানঃ

সূচকের ধারনার সাহায্যে প্রদত্ত শর্তানুসারে ৫ দিনে কোভিড আক্রান্তের একটি ছক নিন্মে প্রস্তুত করিঃ

দিন	আক্রান্ত রোগীর সংখ্যার গুণাকার	আক্রান্ত রোগীর সংখ্যার সূচকীয় আকার
১ম	৩	৩১
২য়	৩×৩	৩২
৩য়	৩×৩×৩	৩৩
৪র্থ	৩×৩×৩×৩	৩৪
৫ম	৩×৩×৩×৩×৩	৩৫

অতএব, ৫ম দিনে কোভিড আক্রান্ত লোক থাকবে ৩^৫ জন।

এবং, এই ধারায় ১১তম ও ১৪তম দিন শেষে সর্বনিন্ম আক্রান্ত রোগী থাকবে যথাক্রমে ৩^১১ জন ও ৩^১৪ জন।

২) খালি ঘরগুলো সঠিকভাবে পূরণ করঃ

সমাধানঃ

১ম অংশের সমাধানঃ

সূচকের গুণ	গুণফল
৮৫×৮৯	৮১৪
১৪৮×১৪১৪	১৪২২
৫১৪×৫১৫	৫২৯
১৭১০×১৭৬	১৭১৬
১৮২১×১৮৬৭	১৮৮৮

২য় অংশের সমাধানঃ

সূচকের ভাগ	ভাগফল
৯৫৮÷৯৩৭	৯২১
১১১২÷১১৪	১১৮
৪৩৫÷৪৬	৪২৯
৫২৮÷৫২৮	৫২০
৪৭২১÷৪৭২৫	৪৭-৩
১৯১০÷১৯৬৭	১৭-৫৭

৩য় অংশের সমাধানঃ

সূচকের সূচকাকার	সূচকের সংক্ষিপ্ত আকার
(১৬৩)৮	১৬২৪
(২৬২)৬	২৬১২
(৩৪)১১	৩৪৪
(৫৪)-৫	৫-২০
(১৫-৭)-২	১৫১৪

৩) ১০ হাজার, ১ লক্ষ, ১০ লক্ষ, ১ কোটি এবং ১০ কোটি সংখ্যাগুলোকে গাণিতিক ভাষায় ছোট আকারে প্রকাশ করো। দেখো তো মূল সংখ্যায় ১ এর ডানে মোট কতটি শূণ্য রয়েছে। এবার সংখ্যাটিকে ছোট আকারে প্রকাশের পর, যে সূচকীয় সংখ্যাটি পাও, তার সাথে পূর্বের প্রাপ্ত শুণ্যের সংখ্যার মাঝে কোন সম্পর্ক পাওয়া যায় কী?

সমাধানঃ

১০ হাজার

= ১০০০০

= ১০০০×১০^১

= ১০০×১০^২

= ১০×১০^৩

= ১×১০^৪

একইভাবে পাই,

১ লক্ষ = ১০০০০০ = ১×১০^৫

১০ লক্ষ = ১০০০০০০ = ১×১০^৬

১ কোটি = ১০০০০০০০ = ১×১০^৭

১০ কোটি = ১০০০০০০০০ = ১×১০^৮

এখানে, মূল সংখ্যায় ১ এর ডানে যতগুলো শূন্য আছ তার মান সংখ্যাটিকে ছোট আকারে প্রকাশের পর যে সূচকীয় সংখ্যাটি পাই সেখানে  ১০ এর সূচকের মান এর সমান। এটাই নির্ণেয় সম্পর্ক।

উক্ত সম্পর্ককে ছক আকারে দেখানো হলোঃ

মূল সংখ্যা	সূচকীয় আকার	মূল সংখ্যায় ১ এর ডানে শূণ্য সংখ্যা	সূচকীয় সংখ্যায় ১০ এর সূচকের মান
১০,০০০	১×১০৪	৪	৪
১,০০,০০০	১×১০৫	৫	৫
১০,০০,০০০	১×১০৬	৬	৬
১,০০,০০,০০০	১×১০৭	৭	৭
১০,০০,০০,০০০	১×১০৮	৮	৮