
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর সপ্তম অধ্যায় বাইনারি সংখ্যার গল্প, সম্পর্কে।
বাইনারি সংখ্যার গল্প
আমরা যখন কোন কিছু যখন গণনা করি তখন ১,২,৩,৪,…….. এর এই ধারাবাহিক গণনার ধারা অনুসরন করি আর এই পদ্ধতিকে বলা হয় দশমিক পদ্ধতি কারন এই পদ্ধতিতে ১০টি অঙ্ক ব্যবহার করা হয়। সেগুলো হলোঃ ০,১,২,৩,৪,৫,৬,৭,৮ এবং ৯। কিন্তু আমাদের চারপাশের সকল কম্পিউটার, ক্যালকুলেটর বা অন্যান্য যন্ত্রগুলো শুধুমাত্র দুইটি অঙ্ক ব্যবহার করে গণনা বা অন্যান্য কাজ করতে পারে। সেই অঙ্ক দুটি হলো ০ ও ১। কম্পিউটার যেহেতু বিদ্যুৎ দ্বারা চালিত তাই সেগুলো শুধু বিদ্যুতের উপস্থিতি ও অনুপস্থিতিকে সংকেত হিসেবে বিবেচনা করে চালিত হয় আর এই অন বা অফ এর প্রকাশ ১ ও ০ এর দ্বারা হয়ে থাকে। কম্পিউটারের এই গণনা পদ্ধতিকে বলা হয় বাইনারি সংখ্যার পদ্ধতি। এই পদ্ধতির বিভিন্ন প্রকার শিখন নিয়ে সাজানো আমাদের আজকের গল্পের নাম বাইনারি সংখ্যার গল্প।
দশমিক পদ্ধতিতে আমরা ০-৯ পর্যন্ত চিহ্নগুলোকে অঙ্ক বা digit বলি। আর বাইনারির ০ এবং ১-কে বাইনারি অঙ্ক বা Binary Digit বলা হয়। বার বার Binary Digit না বলে Binary হতে Bi আর Digit-এর t মিলিয়ে সংক্ষেপে বলা হয় Bit. বাংলায় আমরা একে বিট লিখি। দুই-ভিত্তিক সংখ্যা পদ্ধতিতে ০ আর ১ ছাড়া আর কোন অঙ্ক নেই।
কার্ডে ডট গুণে বাইনারি সংখ্যার গল্পঃ
নিয়মঃ কার্ডগুলোতে নিচের নিয়মে ডট সংখ্যা থাকবে
১ম কার্ডেঃ ১টি ডট
২য় কার্ডেঃ ২টি ডট
৩য় কার্ডেঃ ৪টি ডট
৪র্থ কার্ডেঃ ৮টি ডট
[পুর্বের কার্ডের ডট পরের কার্ডে দ্বিগুন হবে]
…………………এভাবে চলবে।
এখন, সংখ্যা গণনার ক্ষেত্রে,
১ এর বেলায় ১ম কার্ডে একটি ডট অর্থাৎ ১ম কার্ডকে অন আর বাকি কার্ডগুলো অফ ধরতে হবে।
২ এর বেলায় ২য় কার্ডে দুইটি ডট অর্থাৎ ২য় কার্ডকে অন আর বাকি কার্ডগুলো অফ ধরতে হবে।
৩ এর বেলায় ১ম কার্ডে ১টি ও ২য় কার্ডে ২টি ডট অর্থাৎ ১ম ও ২য় কার্ডকে অন আর বাকি কার্ডগুলো অফ ধরতে হবে।
এভাবে চলবে…..
অর্থাৎ দশমিক সংখ্যার সাথে মিল রেখে কোন কোন কার্ডের ডট অন থাকবে তা হিসাব করতে হবে এবং অফ কার্ডকে ০ ও অন কার্ডকে ১ ধরে সংখ্যা গঠন করলে সেটি হবে বাইনারি সংখ্যা।
শিখনঃ
ছবিটি দেখে প্রতিটি কার্ডের নিচে অন বা অফ এবং সেই অনুসারে ১ বা ০ বসিয়ে নিচের ফাঁকা কাজটি করো।
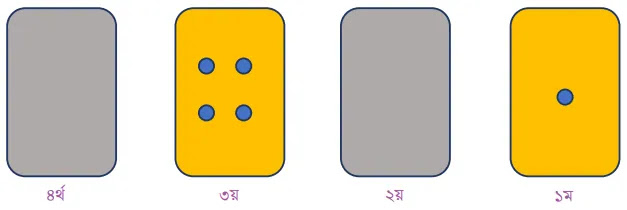
ফাঁকা কাজঃ
| কার্ডের ক্রম | ৪র্থ | ৩য় | ২য় | ১ম |
| অন বা অফ | ||||
| ১ বা ০ |
সমাধানঃ
| কার্ডের ক্রম | ৪র্থ | ৩য় | ২য় | ১ম |
| অন বা অফ | অফ | অন | অফ | অন |
| ১ বা ০ | ০ | ১ | ০ | ১ |
অন কার্ডগুলো মিলিয়ে সর্বমোট ডটের সংখ্যাঃ ০১০১
তার মানে দাঁড়ালোঃ দশমিক সংখ্যা ৫ এর বাইনারি প্রকাশ ০১০১।
শিখনঃ
১ম কার্ড থেকে শেষ কার্ড পর্যন্ত ডটের ধারা হবেঃ ১,২,৪,৮,১৬,……
সেই হিসাবে, ৫টি ডট আছে এমন কোন কার্ড নেই।
তাই ৫টি ডট বানাতে হলে, ১ম কার্ড ও ৩য় কার্ড ব্যবহার করতে হবে। ১ম ও ৩য় কার্ডের ডটের সংখ্যা = ১ + ৪ = ৫।
জোড়ায় কাজ
এবার তাহলে দশমিক সংখ্যা ৩-কে বাইনারিতে কীভাবে প্রকাশ করা যায়, কার্ড এবং ডটের সাহায্যে তা বের করে দেখাও। নিচের ছকটি ব্যবহার করতে পারো। তোমার ডট বসানোর সুবিধার জন্য কার্ডগুলো ফাঁকা রাখা হয়েছে। সঠিক কার্ডে সঠিক সংখ্যক ডট বসাও এবং কার্ডের নিচে অবস্থিত ফাঁকা ঘর পূরণ করোঃ
সমাধানঃ
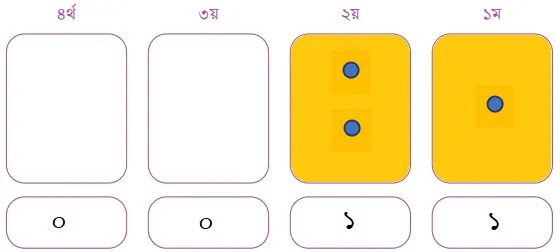
তাহলে, ৩ এর বাইনারি প্রকাশ হলোঃ ০০১১
শিখন প্রশ্নঃ
এবার তবে সংখ্যা ও ডট ব্যবহার করে নিচের সমস্যাগুলো সমাধান করোঃ
১। দশমিক সংখ্যা ৬ এর বাইনারি মান কত?
২। দশমিক সংখ্যা ৯ এর বাইনারি মান কত?
সমাধানঃ
(১)
৬ এর বাইনারি মান বের করার জন্য বিভিন্ন ডট বিশিষ্ট কার্ডের ধাপ নিন্মরুপঃ
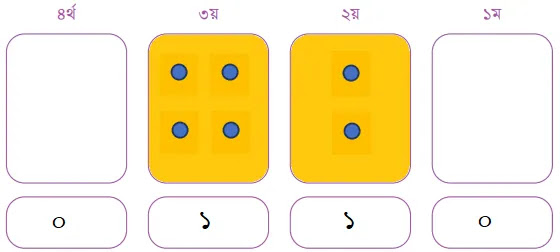
তাহলে, দশমিক সংখ্যা ৬ এর বাইনারি মান ০১১০।
(২)
৯ এর বাইনারি মান বের করার জন্য বিভিন্ন ডট বিশিষ্ট কার্ডের ধাপ নিন্মরুপঃ
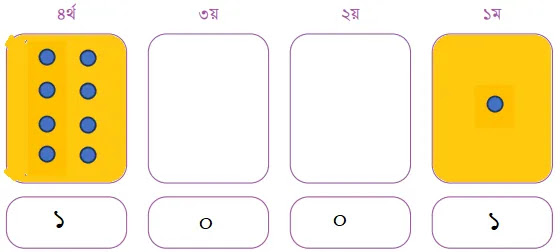
তাহলে, দশমিক সংখ্যা ৯ এর বাইনারি মান ১০০১।
একক কাজ:
নিচের ছকের ফাঁকা ঘরগুলো সঠিক দশমিক সংখ্যা, কার্ড বা বাইনারি সংখ্যা দিয়ে পূরণ করো।
সমাধানঃ
প্রদত্ত ছকটি নিচে পূরণ করে দেখানো হলোঃ
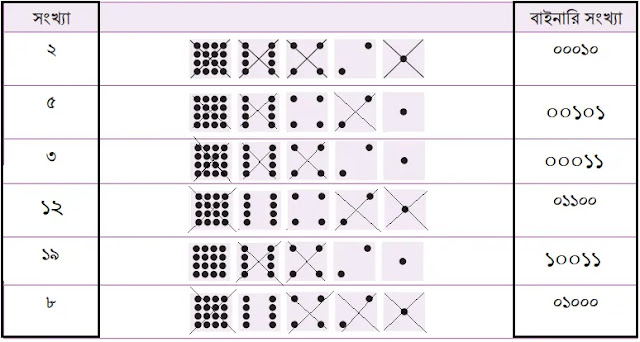
কার্ড ব্যবহার না করে বাইনারি সংখ্যা গণনাঃ
কার্ডব্যবহার করার ক্ষেত্রে দেখেছি যে ডট দেখা গেলে ১ আর না দেখা গেলে ০ ধরা হচ্ছে, এবং প্রতিটি কার্ডের ডটের সংখ্যা আগের কার্ডটিরতে থাকা ডটের সংখ্যার দ্বিগুণ। তা-ই যদি হয়, তাহলে আমরা ডট ব্যবহার না করে কেবল অন বা অফ ধরি। আর অন-অফ বুঝানোর ক্ষেত্রে লাইট বাল্বের থেকে ভালো কী আছে? তাহলে এসো, এবার ডট বাদ দিয়ে একই গণনা করা যায় কিনা দেখি। নিচের ছবিতে দেখো, কার্ডের বদলে বাল্ব ব্যবহার করে অন করে রাখা হয়েছে এবং ডটের সংখ্যার বদলে সরাসরি সংখ্যা ব্যবহার করা হয়েছে।
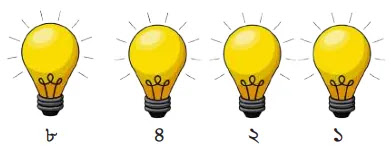
উপরের ছবিটিতে ১ম থেকে ৪র্থ সব কয়টি অবস্থানই অন আছে। এবার ছবিটি দেখে একটু চিন্তা করে নিচের প্রশ্নগুলোর সঠিক উত্তর দাও।
কুইজ
১। উপরের ছবিটিতে বাইনারিতে কোন সংখ্যাটি প্রকাশ করা হয়েছে?
ক. ১০১১
খ. ১১১১
গ. ১১০১
ঘ. ১০০০
উত্তরঃ ১১১১
২। উপরের ছবিটিতে যে বাইনারি সংখ্যাটি দেখানো হয়েছে তার দশমিক মান কত?
ক. ১১
খ. ১০
গ. ১৫
ঘ. ১৬
উত্তরঃ ১৫
সমস্যা ১। নিচের ছবি দেখে বাইনারি এবং দশমিক সংখ্যা নির্ণয় করো এবং ফাঁকা ঘরে লেখো।

সমাধানঃ
বাইনারিঃ ০১১১
দশমিকঃ ৭ [ব্যাখ্যাঃ ৪+২+১ = ৭]
সমস্যা ২। যে সংখ্যাটি বাইনারিতে ১১০১, সেটিকে দশমিকে প্রকাশ করলে কত আসবে?
সমাধানঃ
দশমিকঃ ১৩
সমস্যা ৩। দশমিক সংখ্যা ১৩ কে বাইনারিতে প্রকাশ করলে কত আসবে?
সমাধানঃ
বাইনারিঃ ১১০১
সমস্যা ৪। বাইনারিতে ১০১ কত বিটের সংখ্যা?
উত্তরঃ বাইনারিতে ১০১ হলো ৩ বিটের সংখ্যা।
সমস্যা ৫। দশমিক সংখ্যা ১২ কে বাইনারিতে প্রকাশ করলে কত হবে? সেটি কত বিটের সংখ্যা?
সমাধানঃ
দশমিক হতে বাইনারিতে প্রকাশঃ
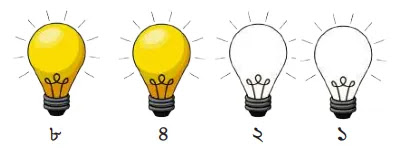
চিত্র হতেঃ ১২ = ৮+৪ এবং বাল্বের অফ কে ০ও অনকে ১ ধরে পাই, ১১০০।
অতএব, দশমিক সংখ্যা ১২ কে বাইনারিতে প্রকাশ করলে হয় ১১০০।
এখন, ১১০০ তে বিট আছে ৪টি।
অতএব, সংখ্যাটি ৪ বিটের সংখ্যা।
মগজ খাটাও বাইনারি সংখ্যার গল্প বোঝঃ
মাথা খাটিয়ে নিচের প্রশ্নগুলোর ঝটপট উত্তর দাও দেখি।
১। ৪টি বিট দিয়ে বাইনারিতে সর্বোচ্চ কত পর্যন্ত গণনা করা যাবে? দশমিকে সেই সংখ্যাটি কত?
সমাধানঃ
বাইনারিতে অঙ্ক সংখ্যা হলো ০ ও ১ যেখানে ১ > ০। তাহলে, চার অঙ্কের সর্বোচ্চ বাইনারি সংখ্যা হবে ১১১১।
অর্থাৎ, ৪টি বিট দিয়ে বাইনারিতে সর্বোচ্চ ১১১১ পর্যন্ত গণনা করা যাবে।
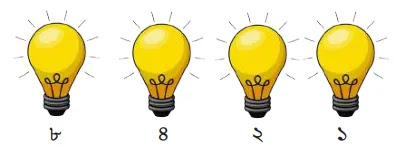
এখন, এখন চার বিটের বাইনারি সংখ্যার ক্ষেত্রে উপরের চিত্র অনুসারে দশমিক সংখ্যাটি হবে = ৮+৪+২+১ = ১৫।
২। ২ বিট দিয়ে বাইনারিতে সর্বোচ্চ কত সংখ্যা বানাতে পারবে? দশমিকে সেই সংখ্যাটি কত?
সমাধানঃ
বাইনারিতে অঙ্ক সংখ্যা হলো ০ ও ১ যেখানে ১ > ০। তাহলে, দুই অঙ্কের সর্বোচ্চ বাইনারি সংখ্যা হবে ১১।
এখন,
বাইনারি ১১ এর দশমিক সংখ্যা হলো ৩।
অতএব, ২ বিট দিয়ে বাইনারিতে সর্বোচ্চ (৩+১)=৪টি সংখ্যা বানাতে পারবো।
৩। দশমিকে ৪ বাইনারিতে কত বিটের সংখ্যা?
সমাধানঃ
দশমিকে ৪ = বাইনারিতে ১০০।
অতএব, দশমিকে ৪ বাইনারিতে ৩ বিটের সংখ্যা।
৪। ৫ বিট দিয়ে বাইনারিতে সর্বোচ্চ কত সংখ্যা বানাতে পারবে? দশমিকে সেই সংখ্যাটি কত?
সমাধানঃ
বাইনারিতে অঙ্ক সংখ্যা হলো ০ ও ১ যেখানে ১ > ০। তাহলে, দুই অঙ্কের সর্বোচ্চ বাইনারি সংখ্যা হবে ১১১১১।
এখন,
বাইনারি ১১১১১ এর দশমিক সংখ্যা হলো ৩১।
অতএব, ৫ বিট দিয়ে বাইনারিতে সর্বোচ্চ (৩১+১)=৩২টি সংখ্যা বানাতে পারবো যেখানে সর্বনিন্ম সংখ্যা ০ ও সর্বোচ্চ সংখ্যা ৩১।
৫। ৮ম বিটে কয়টি ডট?
সমাধানঃ
৮ম বিটে ডট আছে ২৭ টি= ১২৮ টি।
কার্ড ও বাল্বের সাহায্যে বাইনারি মান নির্ণয় – ৭ম অধ্যায় ( ১৫১ – ১৫৩ পৃষ্ঠা)
কার্ড ও বাল্বের সাহায্যে বাইনারি মান নির্ণয়
দলগত কাজ: তোমরা ৪ জনের দল তৈরি করে ০ থেকে ১৫ পর্যন্ত সংখ্যাগুলোর বাইনারি মান কার্ড এবং বাল্বের সাহায্যে নির্ণয় করো।
সমাধানঃ
কার্ডের সাহায্যে ০ থেকে ১৫ সংখ্যাগুলোর বাইনারি মান নির্ণয়ঃ
| সংখ্যা | প্রতি সারিতে ৪টি করে কার্ড এবং কার্ড অনুসারে ডট, অন কার্ডগুলো হলুদ এবং অফ কার্ডগুলো অফ হোয়াইট দেখিয়ে অন এর জন্য ১ ও অফ এর জন্য ০ ধরা হয়েছে। | বাইনারি মান | |||
| ০ | ●●●●●●●● | ●●●● | ●● | ● | ০০০০ |
| ০ | ০ | ০ | ০ | ||
| ১ | ●●●●●●●● | ●●●● | ●● | ● | ০০০১ |
| ০ | ০ | ০ | ১ | ||
| ২ | ●●●●●●●● | ●●●● | ●● | ● | ০০১০ |
| ০ | ০ | ১ | ০ | ||
| ৩ | ●●●●●●●● | ●●●● | ●● | ● | ০০১১ |
| ০ | ০ | ১ | ১ | ||
| ৪ | ●●●●●●●● | ●●●● | ●● | ● | ০১০০ |
| ০ | ১ | ০ | ০ | ||
| ৫ | ●●●●●●●● | ●●●● | ●● | ● | ০১০১ |
| ০ | ১ | ০ | ১ | ||
| ৬ | ●●●●●●●● | ●●●● | ●● | ● | ০১১০ |
| ০ | ১ | ১ | ০ | ||
| ৭ | ●●●●●●●● | ●●●● | ●● | ● | ০১১১ |
| ০ | ১ | ১ | ১ | ||
| ৮ | ●●●●●●●● | ●●●● | ●● | ● | ১০০০ |
| ১ | ০ | ০ | ০ | ||
| ৯ | ●●●●●●●● | ●●●● | ●● | ● | ১০০১ |
| ১ | ০ | ০ | ১ | ||
| ১০ | ●●●●●●●● | ●●●● | ●● | ● | ১০১০ |
| ১ | ০ | ১ | ০ | ||
| ১১ | ●●●●●●●● | ●●●● | ●● | ● | ১০১১ |
| ১ | ০ | ১ | ১ | ||
| ১২ | ●●●●●●●● | ●●●● | ●● | ● | ১১০০ |
| ১ | ১ | ০ | ০ | ||
| ১৩ | ●●●●●●●● | ●●●● | ●● | ● | ১১০১ |
| ১ | ১ | ০ | ১ | ||
| ১৪ | ●●●●●●●● | ●●●● | ●● | ● | |
| ১ | ১ | ১ | ০ | ১১১০ | |
| ১৫ | ●●●●●●●● | ●●●● | ●● | ● | ১১১১ |
| ১ | ১ | ১ | ১ | ||
বাল্বের সাহায্যে ০ থেকে ১৫ সংখ্যাগুলোর বাইনারি মান নির্ণয়ঃ
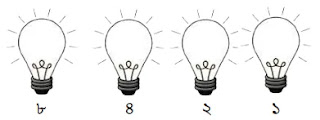
উপরের চিত্রে ০ এর জন্য একটাও বাল্ব অন থাকে না, অফ বাল্বের জন্য ০ ধরে পাই ০০০০।
অতএব, ০ এর বাইনারি মান = ০০০০।
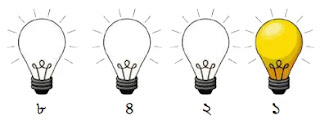
উপরের চিত্রে ১ এর জন্য শুধুমাত্র ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০০০১।
অতএব, ১ এর বাইনারি মান = ০০০১।
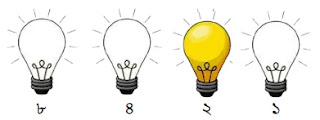
উপরের চিত্রে ২ এর জন্য শুধুমাত্র ২য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০০১০।
অতএব, ২ এর বাইনারি মান = ০০১০।
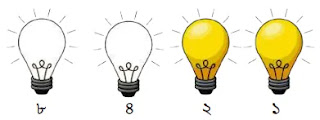
উপরের চিত্রে ৩ এর জন্য শুধুমাত্র ১ম ও ২য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০০১১।
অতএব, ৩ এর বাইনারি মান = ০০১১।
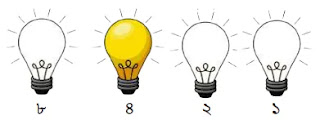
উপরের চিত্রে ৪ এর জন্য শুধুমাত্র ৩য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০১০০।
অতএব, ৪ এর বাইনারি মান = ০১০০।
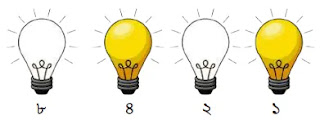
উপরের চিত্রে ৫ এর জন্য শুধুমাত্র ৩য় ও ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০১০১।
অতএব, ৫ এর বাইনারি মান = ০১০১।
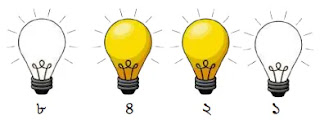
উপরের চিত্রে ৬ এর জন্য শুধুমাত্র ৩য় ও ২য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০১১০।
অতএব, ৬ এর বাইনারি মান = ০১১০।
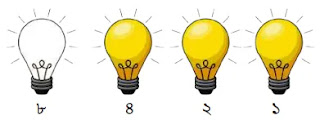
উপরের চিত্রে ৭ এর জন্য শুধুমাত্র ৩য়, ২য় ও ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ০১১১।
অতএব, ৭ এর বাইনারি মান = ০১১১।
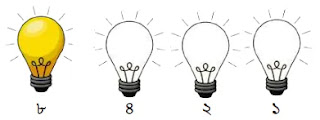
উপরের চিত্রে ৮ এর জন্য শুধুমাত্র ৪র্থ বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১০০০।
অতএব, ৮ এর বাইনারি মান = ১০০০।
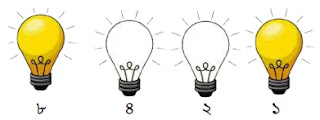
উপরের চিত্রে ৯ এর জন্য শুধুমাত্র ৪র্থ ও ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১০০১।
অতএব, ৯ এর বাইনারি মান = ১০০১।
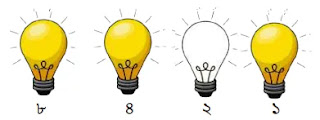
উপরের চিত্রে ১০ এর জন্য শুধুমাত্র ৪র্থ ও ২য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১০১০।
অতএব, ১০ এর বাইনারি মান = ১০১০।
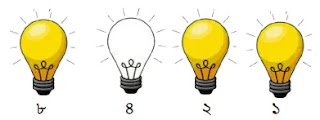
উপরের চিত্রে ১১ এর জন্য শুধুমাত্র ৪র্থ, ২য় ও ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১০১১।
অতএব, ১১ এর বাইনারি মান = ১০১১।
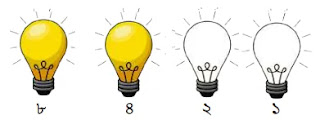
উপরের চিত্রে ১২ এর জন্য শুধুমাত্র ৪র্থ ও ৩য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১১০০।
অতএব, ১২ এর বাইনারি মান = ১১০০।

উপরের চিত্রে ১৩ এর জন্য শুধুমাত্র ৪র্থ, ৩য় ও ১ম বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১১০১।
অতএব, ১৩ এর বাইনারি মান = ১১০১।
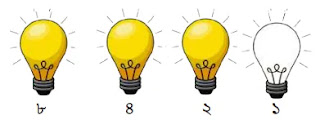
উপরের চিত্রে ১৪ এর জন্য শুধুমাত্র ৪র্থ, ৩য় ও ২য় বাল্ব অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১১১০।
অতএব, ১৪ এর বাইনারি মান = ১১১০।
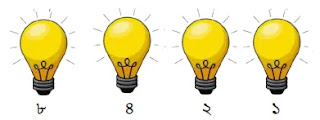
উপরের চিত্রে ১৫ এর জন্য চারটি বাল্বই অন থাকে। অন বাল্বের জন্য ১ ও অফ বাল্বের জন্য ০ ধরে পাই ১১১১।
অতএব, ১৫ এর বাইনারি মান = ১১১১।
আরেকটু ভেবে দেখিঃ
তুমি যদি বিভিন্ন বিট সংখ্যার জন্য সর্ববামের কার্ডে ডটের সংখ্যা এবং ঐ সংখ্যক বিট দিয়ে সর্বোচ্চ সম্ভব সংখ্যা নির্ণয় করতে পারো, তবে আগের পৃষ্ঠার সমস্যাগুলো সমাধান করা তোমার জন্য আরও সহজ হয়ে যাবে। নিচের ছকটি পূরণ করে সহজেই উত্তরগুলো লিখতে পারো। কয়েকটি তোমার জন্য পূরণ করে দেওয়া আছে।
| বিট সংখ্যা (কার্ড সংখ্যা) | সর্ববামের ডটের সংখ্যা | সর্বোচ্চ কোন দশমিক সংখ্যা তৈরি করা সম্ভব |
| ১ | ১ | ১ |
| ২ | ২ | ৩ |
| ৩ | ৪ | ৭ |
| ৪ | ৮ | ১৫ |
| ৫ | ১৬ | ৩১ |
| ৬ | ৩২ | ৬৩ |
| ৭ | ৬৪ | ১২৭ |
| ৮ | ১২৮ | ২৫৫ |
কুইজ
উপরের ছকটি মনোযোগ দিয়ে পর্যবেক্ষণ করো। এবার বলো, যে কোন একটি বিট সংখ্যা ও তার জন্য সর্বোচ্চ কোন দশমিক সংখ্যা তৈরি করা সম্ভব এদের মধ্যে কি কোন সম্পর্ক আছে? কোন সূত্র বানাতে পারবে সহজেই বিট সংখ্যা থেকে সর্বোচ্চ দশমিক সংখ্যা বের করার জন্য?
সমাধানঃ
একটি বিট সংখ্যা ও তার জন্য যে সর্বোচ্চ দশমিক সংখ্যা তৈরি করা সম্ভব এদের মধ্যে একটি সম্পর্ক আছে। সহজেই বিট সংখ্যা থেকে সর্বোচ্চ দশমিক সংখ্যা বের করার জন্য আমি একটি সূত্র বানাতে পেরেছি। সূত্রটি নিন্মরুপঃ
২বিট সংখ্যা – ১ = সর্বোচ্চ দশমিক সংখ্যা।
উদাহরণঃ
বিট সংখ্যা ১ হলে, সর্বোচ্চ দশিমক সংখ্যা = ২১ – ১ = ২-১ = ১।
বিট সংখ্যা ২ হলে, সর্বোচ্চ দশিমক সংখ্যা = ২২ – ১ = ৪-১ = ৩।
বিট সংখ্যা ৩ হলে, সর্বোচ্চ দশিমক সংখ্যা = ২৩ – ১ = ৮-১ = ৭।
এভাবে সকল ক্ষেত্রে এই সূত্র প্রযোজ্য হবে।
শিখনঃ ২য় বিট পর্যন্ত ব্যবহার করে কী কী সংখ্যা তৈরি করা যায়?
সমাধানঃ
২য় বিট পর্যন্ত ব্যবহার করে গঠিত বাইনারি সংখ্যাগুলো হলোঃ
০০, ০১, ১০, ১১।
অর্থাৎ ২য় বিট পর্যন্ত ব্যবহার করে মোট ৪টি সংখ্যা তৈরি করা যায়।
শিখনঃ বিট ১-৮ পর্যন্ত ব্যবহার করে মোট কতটি সংখ্যা পাওয়া যায় তার ছকটি পূরণ করো।
সমাধানঃ
| বিট সংখ্যা (কার্ড সংখ্যা) | মোট কতটি সংখ্যা পাওয়া সম্ভব (০ সহ) |
| ১ | ২ |
| ২ | ৪ |
| ৩ | ৮ |
| ৪ | ১৬ |
| ৫ | ৩২ |
| ৬ | ৬৪ |
| ৭ | ১২৮ |
| ৮ | ২৫৬ |
শিখন ফলাফলঃ এই নিয়ম ২বিট সংখ্যা = মোট গঠিত সংখ্যা।
পরবর্তী পৃষ্ঠার সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

