
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর সপ্তম অধ্যায় বাইনারি সংখ্যার গল্প, সম্পর্কে।
হাতের আঙুলে বাইনারি গণনা, দৈর্ঘ্য ও ভর মাপার চ্যালেঞ্জ – ৭ম অধ্যায় ( ১৫৩ – ১৫৭ পৃষ্ঠা)
হাতের আঙুলে বাইনারি গণনা
এই পদ্ধতিতে আঙুল খোলা থাকা মানেই অন। আর গুটিয়ে রাখলে অফ। প্রথমে ডান হাতের আঙ্গুলগুলো ব্যবহার করি। তোমার বুড়ো আঙ্গুলটিকে ধরো ১ম বিট। তর্জনিটি হোক ২য় বিট। মধ্যমা ৩য় বিট। অনামিকা হোক ৪র্থ বিট। এবং কনিষ্ঠা ৫ম বিট। কোন বিটে কতটি ডট তা পূর্বের থেকে স্মরণ করো বা নিচের ছবি থেকে দেখ।
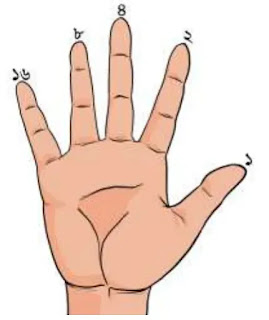
অর্থাৎ, হাতের আঙুলে বাইনারি গণনা হলো পূর্বের কার্ড বা বাল্ব এর অনুরুপ শুধুমাত্র এখানে অন বা অফ বোঝাতে আঙ্গুলটি খোলা আছে কিনা তাই মূখ্য।
একক কাজঃ
দৈর্ঘ্য মাপার চ্যালেঞ্জঃ
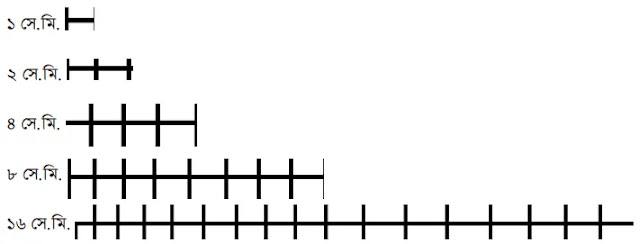
উপরের চিত্রে ১ সে.মি., ২ সে.মি., ৪ সে.মি., ৮ সে.মি. ও ১৬ সে.মি. দৈর্ঘ্য দেখানো আছে। এই দৈর্ঘ্যগুলির সমান কাগজ/কাঠি কেটে নাও। এরপর সেগুলি মাত্র একবার করে নিয়ে ০ সে.মি. থেকে ৩১ সে.মি পর্যন্ত প্রতিটি দৈর্ঘ্য পরিমাপ করা যায় কিনা দেখো। কীভাবে পরিমাপ করা যায় তা নিচের সারণিতে লেখো।
সমাধানঃ
১ সে.মি., ২ সে.মি., ৪ সে.মি., ৮ সে.মি. ও ১৬ সে.মি. দৈর্ঘ্য বিশিষ্ট কাঠি কেটে নিলাম এবং পরে ০ থেকে ৩১ সেমি দৈর্ঘ্য উক্ত কাঠি দ্বারা মেপে দেখলাম। ফলে সেক্ষেত্রে যে যে কাঠি ব্যবহার করেছি তার জন্য “হ্যাঁ” ও ব্যবহার না করলে তার জন্য “না” লিখে সারণিটি পূরণ করলাম।
| দৈর্ঘ্য (সেমি) | ১৬ সেমি | ৮ সেমি | ৪ সেমি | ২ সেমি | ১ সেমি |
| ০ | না | না | না | না | না |
| ১ | না | না | না | না | হ্যাঁ |
| ২ | না | না | না | হ্যাঁ | না |
| ৩ | না | না | না | হ্যাঁ | হ্যা |
| ৪ | না | না | হ্যাঁ | না | না |
| ৫ | না | না | হ্যাঁ | না | হ্যাঁ |
| ৬ | না | না | হ্যাঁ | হ্যাঁ | না |
| ৭ | না | না | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ৮ | না | হ্যাঁ | না | না | না |
| ৯ | না | হ্যাঁ | না | না | হ্যাঁ |
| ১০ | না | হ্যাঁ | না | হ্যাঁ | না |
| ১১ | না | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| ১২ | না | হ্যাঁ | হ্যাঁ | না | না |
| ১৩ | না | হ্যাঁ | হ্যাঁ | না | হ্যাঁ |
| ১৪ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ | না |
| ১৫ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ১৬ | হ্যাঁ | না | না | না | না |
| ১৭ | হ্যাঁ | না | না | না | হ্যাঁ |
| ১৮ | হ্যাঁ | না | না | হ্যাঁ | না |
| ১৯ | হ্যাঁ | না | না | হ্যাঁ | হ্যাঁ |
| ২০ | হ্যাঁ | না | হ্যাঁ | না | না |
| ২১ | হ্যাঁ | না | হ্যাঁ | না | হ্যাঁ |
| ২২ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | না |
| ২৩ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ২৪ | হ্যাঁ | হ্যাঁ | না | না | না |
| ২৫ | হ্যাঁ | হ্যাঁ | না | না | হ্যাঁ |
| ২৬ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | না |
| ২৭ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| ২৮ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | না |
| ২৯ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ |
| ৩০ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না |
| ৩১ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ |
শিখনঃ এ সারণি তৈরি করতে গিয়ে মিনা নিচের ধারণাগুলি পেয়েছে। তুমি মিনার ধারণাগুলির সাথে একমত কিনা সেটা কারণসহ লিখে সারণি পূরণ করো।
সমাধানঃ
মিনার ধারণা উল্লেখপূর্বক কারনসহ সারণিটি নিচে পূরণ করে দেখানো হলোঃ
| মিনার ধারণা | তুমি কি মিনার সাথে একমত | কারণ |
| ২৫ সেমি দৈর্ঘ্য পরিমাপ করা সম্ভব নয়। | না | ১৬ সেমি + ৮ সেমি + ১ সেমি = ২৫ সেমি। কাজেই ২৫ সেমি পরিমাপ করা সম্ভব। |
| ১২ সেমি দৈর্ঘ্য পরিমাপ করতে ২ সেমি দৈর্ঘ্য প্রয়োজন হয় না। | হ্যাঁ | ৮ সেমি + ৪ সেমি = ১২ সেমি। কাজেই ১২ সেমি পরিমাপে ২ সেমি দৈর্ঘ্য প্রয়োজন হয় না। |
| ২২ সে.মি দৈর্ঘ্য পরিমাপ করতে ৮ সে.মি দৈর্ঘ্য প্রয়োজন হয় না। | হ্যাঁ | ১৬ সেমি + ৪ সেমি + ২ সেমি = ২২ সেমি। কাজেই ২২ সেমি পরিমাপে ৮ সেমি দৈর্ঘ্য প্রয়োজন হয় না। |
| ১৫ সে.মি দৈর্ঘ্য পরিমাপ করতে ১৬ সে.মি দৈর্ঘ্য প্রয়োজন হয় না। | হ্যাঁ | ৮ সেমি + ৪ সেমি + ২ সেমি + ১ সেমি = ১৫ সেমি। কাজেই ১৫ সেমি পরিমাপে ১৬ সেমি দৈর্ঘ্য প্রয়োজন হয় না। |
| ১ সে.মি, ২ সে.মি. ও ৪ সে.মি দৈর্ঘ্য ব্যবহার করে সর্বোচ্চ ১২ সে.মি দৈর্ঘ্য পর্যন্ত মাপা যায়। | না | ১ সে.মি, ২ সে.মি. ও ৪ সে.মি দৈর্ঘ্য ব্যবহার করে সর্বোচ্চ ৮ সে.মি দৈর্ঘ্য পর্যন্ত মাপা যায়। |
শিখনঃ লক্ষ্য করো, ১৬ সে.মি +৮ সে.মি + ১ সে.মি = ২৫ সে.মি, আবার ২৫ এর বাইনারি প্রকাশঃ ১১০০১। এখান থেকে দৈর্ঘ্য মাপার চ্যালেঞ্জ এর সাথে বাইনারি সংখ্যার কোন মিল খুঁজে পাচ্ছ কি? আরেকবার ০ সে.মি. থেকে ৩১ সে.মি পর্যন্ত দৈর্ঘ্য তৈরির সারণি দেখে নাও। এখন আরো সহজেই বাইনারি সংখ্যা ব্যবহার করে যেকোনো দৈর্ঘ্য তৈরি করতে পারবে কিনা? তাহলে নিচের সারণিটি পূরণ করো সেভাবে।
সমাধানঃ
প্রদত্ত সারণিটি পূরণ করে নিচে দেওয়া হলোঃ
| দৈর্ঘ্য (সেমি) | বাইনারি প্রকাশ | ১৬ সেমি | ৮ সেমি | ৪ সেমি | ২ সেমি | ১ সেমি |
| ২৫ | ১১০০১ | হ্যাঁ | হ্যাঁ | না | না | হ্যাঁ |
| ১ | ১ | ০ | ০ | ১ | ||
| ১১ | ০১০১১ | না | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| ০ | ১ | ০ | ১ | ১ | ||
| ২২ | ১০১১০ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | না |
| ১ | ০ | ১ | ১ | ০ | ||
| ২৩ | ১০১১১ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ১ | ০ | ১ | ১ | ১ |
তাহলে বুঝতেই পারছ যে, কম্পিউটারের ভাষা বাইনারি হলেও শুধু সেখানেই এটা সীমাবদ্ধ নয়। বরং বাইনারি দিয়ে আরো অনেক সমস্যার সহজে সমাধান করা সম্ভব। শুধু পর্যবেক্ষণ করে খজেুঁ নিতে হবে কোথায় বাইনারির ধারণা কাজে লাগানো সম্ভব।
ভর মাপার চ্যালেঞ্জঃ
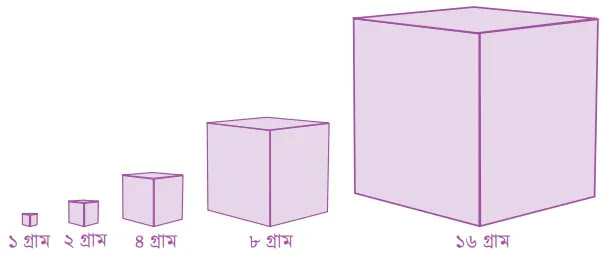
উপরের চিত্রে ১ গ্রাম, ২ গ্রাম, ৪ গ্রাম, ৮ গ্রাম ও ১৬ গ্রাম দেখানো আছে। এই ভরগুলি মাত্র একবার করে নিয়ে ০ গ্রাম থেকে ৩১ গ্রাম পর্যন্ত প্রতিটি ভর পরিমাপ করা যায় কিনা দেখো। কীভাবে পরিমাপ করা যায় তা ‘দৈর্ঘ্য মাপার চ্যালেঞ্জ’ অংশের ন্যায় একটি তালিকা তৈরি করো দেখাও।
সমাধানঃ
১ গ্রাম., ২ গ্রাম, ৪ গ্রাম, ৮ গ্রাম ও ১৬ গ্রাম ভর বিশিষ্ট বাটখারা নিলাম এবং পরে ০ থেকে ৩১ গ্রাম ভরকে উক্ত বাটখারা দ্বারা মেপে দেখলাম। ফলে সেক্ষেত্রে যে যে বাটখারা ব্যবহার করেছি তার জন্য “হ্যাঁ” ও ব্যবহার না করলে তার জন্য “না” লিখে সারণিটি ‘দৈর্ঘ্য মাপার চ্যালেঞ্জ’ অংশের ন্যায় পূরণ করলাম।
| ভর (গ্রাম) | ১৬ গ্রাম | ৮ গ্রাম | ৪ গ্রাম | ২ গ্রাম | ১ গ্রাম |
| ০ | না | না | না | না | না |
| ১ | না | না | না | না | হ্যাঁ |
| ২ | না | না | না | হ্যাঁ | না |
| ৩ | না | না | না | হ্যাঁ | হ্যা |
| ৪ | না | না | হ্যাঁ | না | না |
| ৫ | না | না | হ্যাঁ | না | হ্যাঁ |
| ৬ | না | না | হ্যাঁ | হ্যাঁ | না |
| ৭ | না | না | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ৮ | না | হ্যাঁ | না | না | না |
| ৯ | না | হ্যাঁ | না | না | হ্যাঁ |
| ১০ | না | হ্যাঁ | না | হ্যাঁ | না |
| ১১ | না | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| ১২ | না | হ্যাঁ | হ্যাঁ | না | না |
| ১৩ | না | হ্যাঁ | হ্যাঁ | না | হ্যাঁ |
| ১৪ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ | না |
| ১৫ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ১৬ | হ্যাঁ | না | না | না | না |
| ১৭ | হ্যাঁ | না | না | না | হ্যাঁ |
| ১৮ | হ্যাঁ | না | না | হ্যাঁ | না |
| ১৯ | হ্যাঁ | না | না | হ্যাঁ | হ্যাঁ |
| ২০ | হ্যাঁ | না | হ্যাঁ | না | না |
| ২১ | হ্যাঁ | না | হ্যাঁ | না | হ্যাঁ |
| ২২ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | না |
| ২৩ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| ২৪ | হ্যাঁ | হ্যাঁ | না | না | না |
| ২৫ | হ্যাঁ | হ্যাঁ | না | না | হ্যাঁ |
| ২৬ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | না |
| ২৭ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| ২৮ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | না |
| ২৯ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ |
| ৩০ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না |
| ৩১ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ |
বাইনারি খেলনা/যন্ত্র হতে জীবন বাঁচাতে বাইনারি– ৭ম অধ্যায় ( ১৫৮ – ১৬২ পৃষ্ঠা)
বাইনারি খেলনা/যন্ত্র, জন্মদিনের ম্যাজিক ট্রিক, বাইনারি মোমবাতি, বর্ণের কোড, জীবন বাচাতে বাইনারি
বাইনারি খেলনা কিভাবে বানাতে হয় কিংবা জন্মদিনের ম্যাজিক ট্রিক কেমনে করতে হয় অথবা বাইনারি মোমবাতি দিয়ে কিভাবে সাশ্রয়ী হওয়া যায় এবং ইংরেজি সকল বর্নকে বাইনারি কোডে রুপান্তর কিভাবে করতে হয় এবং জীবন বাঁচানোর জন্য বাইনারির প্রয়োগ সংবলিত সমস্যার সমাধান এই অংশে করা হয়েছে। ধারাবাহিক ভাবে এই অংশে সকল বিষয়াদি তুলে ধরা হয়েছে। তাহলে শুরু করা যাক।
বাইনারি খেলনা/যন্ত্র
বাইনারি সংখ্যা গননার ক্ষেত্রে আমরা যদি হাতের আঙুল ব্যবহার করি তাহলে সর্বোচ্চ দুই হাতের দশটি আঙুল ব্যবহার করতে পারি। যখন সবকটি আঙুল খোলা থাকে তখন ১০টি আঙুল ব্যবহার করলে বাইনারি সংখ্যার হিসাব হয় নিন্মরূপঃ
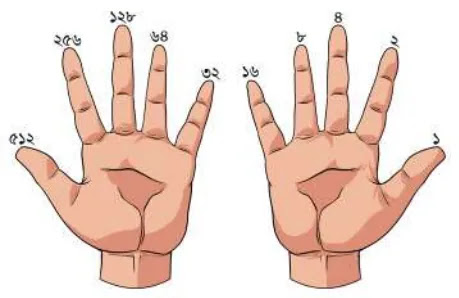
১০টি আঙুল খোলা থাকলে বাইনারি সংখ্যাটি = ১১১১১১১১১১।
এবং দশমিক সংখ্যাটি হবে = ৫১২+২৫৬+১২৮+৬৪+৩২+১৬+৮+৪+২+১ = ১০২৩।
অর্থাৎ আমরা ১০২৩ পর্যন্ত গণনা করতে পারবো দুই হাতের দশটি আঙুল দিয়ে।
শিখনঃ ২০২২ পর্যন্ত গণনা করতে হলে কিন্তু ১০টি আঙুল ব্যবহার যথেষ্ট হবে না। এক্ষেত্রে কী করা যেতে পারে বলে তুমি মনে করো তা লিখোঃ
সমাধানঃ
১) হাতের পাশাপাশি পায়ের আঙ্গুলও গুনতে পারি।
২) কোন বন্ধুকে ডেকে আনতে পারি।
৩) কলম বা পেন্সিল ব্যবহার করতে পারি।
৪) কাগজের টুকরা ব্যবহার করতে পারি।
৫) কাগজে দিয়ে একটা সুন্দর খেলনা/যন্ত্র তৈরি করতে পারি।
[বিঃদ্রঃ কিভাবে কাগজ দিয়ে বাইনারি খেলনা/যন্ত্র তৈরি করতে হয় তা পাঠ্যপুস্তক এর ১৫৯ পৃষ্ঠায় দেখ।]
জন্মদিনের ম্যাজিক ট্রিক
মাজেদুর একজন ম্যাজিশিয়ান। সে যেকারোর জন্মতারিখ বলে দিতে পারে চোখের নিমিষেই। তাঁর কাছে পাচটি কার্ড থাকে। যে কেউ বলে কোন কোন কার্ডে তাঁর জন্ম তারিখ আছে ( যেমন: ২১ শে জুন, ২০১০ বা ২১/৬/২০১০ হলে সেক্ষেত্রে জন্মতারিখ হবে ২১। তাহলেই মাজেদুর চট করে ম্যাজিশিয়ানের মত জন্ম তারিখ বলে দিতে পারে। কিন্তু কীভাবে?
সমাধানঃ
ধরি, আমার জন্ম তারিখ হলো ২১ যা ম্যাজিশিয়ান জানে না। এখন আমি পাঁচটি কার্ড দেখে ম্যাজিশিয়ান কে বললাম আমার জন্ম সংখ্যাটি আছে ৪, ২ ও ০ নং কার্ডে।
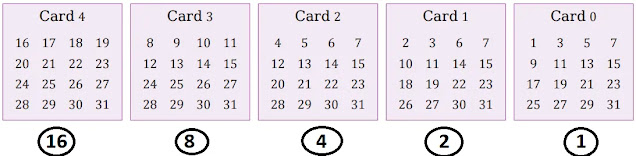
এখন ম্যাজিশিয়্যান ৪, ২ ও ০ কার্ডগুলোকে অন ধরে এবং বাকী কার্ডগুলোকে অফ ধরে সংখ্যা হিসাব করলেই আমার জন্ম তারিখ বেরিয়ে যাবে।
পাঁচটি কার্ডের জন্য বাইনারি মান বের করার ধারাটি হলোঃ ১৬, ৮, ৪, ২, ১। সেক্ষেত্রে ৪, ২ ও ০ কার্ডগুলোকে অন থাকলে সংখ্যাটি হবে ১৬ + ৪ + ১ = ২১ যা আমার জন্মতারিখ।
বাইনারি মোমবাতি অথবা কেকে সাধারণ মোমবাতি
আমরা সাধারণত জন্মদিনের কেকে প্রতি এক বছরের জন্যে একটি মোমবাতি ব্যবহার করি। কিন্তু প্রতিটা মোমবাতি হয় জ্বালানো থাকবে নয়তো নিভানো থাকবে। আমরা এটি ব্যবহার করে তোমার বয়সের বাইনারি পদ্ধতিতে প্রকাশ করতে পারি। উদাহরণস্বরুপ, ১৪ বছর এর বাইনারি ১১১০। তুমি চাইলে মোমবাতির মাধ্যমে প্রকাশ করতে পার।
শিখনঃ
১) বাইনারি মোমবাতী ব্যবহারের সুবিধাগুলো কি কি?
সমাধানঃ
বাইনারি মোমবাতী ব্যবহারের সুবিধাগুলো হলো এক্ষেত্রে সল্প সংখ্যক মোববাতি লাগে এবং সকল মোমবাতি জ্বালানো লাগে না অর্থাৎ এক্ষেত্রে অপচয় রোধ ও খরচ কম হয়।
উদাহরণঃ
ধরি, আমানের বয়স ১৪ বছর। ১৪ এর বাইনারি রুপঃ ১১১০। এখন আমান যদি সাধারন নিয়মে তার জন্মদিনে মোমবাতি ব্যবহার করে তাহলে ১৪ বছরের জন্য মোট ১৪টি মোমবাতি ক্রয় ও জ্বালাতে হবে। কিন্তু বাইনারি মোমবাতী ব্যবহার করলে ১১১০ এর জন্য ৪টি মোমবাতি ক্রয় ও ৩টি জ্বালালেই হবে এবং ১টি জ্বালানোই লাগবে না। অর্থাৎ এক্ষেত্রে অপচয় রোধ ও খরচ কম হবে।
২) বয়স বাড়ার সাথে সাথে কেন বাইনারি মোমবাতী ভালো একটি আইডিয়া হয়?
সমাধানঃ
বয়স বাড়ার সাথে সাথে বাইনারি মোমবাতী ভালো একটি আইডিয়া কারণ জন্মদিনে বাইনারি মোমবাতী ব্যবহারের সুবিধাগুলো হলো এক্ষেত্রে সল্প সংখ্যক মোববাতি লাগে এবং সকল মোমবাতি জ্বালানো লাগে না অর্থাৎ এক্ষেত্রে অপচয় রোধ ও খরচ কম হয়।
উদাহরণঃ
কারো বয়য় ২০ হলে সে জন্মদিনে স্বাভাবিক নিয়মে ২০টি মোমবাতী ব্যবহার না করে ২০ এর বাইনারি ১০১০০ অর্থাৎ ৫টি মোমবাতী ব্যবহারই যথেষ্ট। সেক্ষেত্রে মাত্র ২টি মোববাতী জ্বালো লাগবে আর বাকী ৩টি জ্বালানোই লাগবে না।
৩) বাইনারি মোমবাতি ব্যবহারের অসুবিধা গুলো কি কি? এই অসুবিধা গুলো তুমি কীভাবে অতিক্রম করবে?
সমাধানঃ
বাইনারি মোমবাতি ব্যবহারের অসুবিধা গুলো নিন্মরুপঃ
ক) বাইনারি সংখ্যার ধারণা না থাকা লোকেরা বুঝবে না তোমার বয়স কত?
খ) কিছু মোমবাতি জ্বালানো ও কিছু নেভানো থাকায় অনেকে বিভ্রান্ত হবে।
এই অসুবিধা গুলো আমি যেভাবে অতিক্রম করবঃ
ক) যে মোমবাতীগুলো জ্বালাবো সেগুলোকে ১ ও যেগুলো জ্বালাবো না সেগুলোকে ০ দ্বারা চিহ্নিত করে দিব।
খ) বড় করে বাইনারি পদ্ধতির গণনা উল্লেখসহ এর দশমিক মানও লিখে রাখবো।
এটি কার কেক?
কেক টি কার এটি নিয়ে যে বিভ্রান্তি তৈরী হতে পারে এটির বিস্তারিত বর্ণনা লিখ। কেকটি কে পাবে এর উপসংহার লিখ। সাথে এর কারণ ও লিখ। একটির বেশি সম্ভাব্য ব্যাখ্যা রয়েছে।

সমাধানঃ
চিত্রে মোমবাতী আছে ২টি আবার একটি সংখ্যা ১০ লেখা আছে। অর্থাৎ এখানে একটা বিভ্রান্তি তৈরি হতে পারে যে এটি হয় ২ বছরের বাচ্চার জন্মদিনের কেক নচেৎ ১০ বছরের বাচ্চার জন্মদিনের কেক।
এখন, বাইনারি মোমবাতী পদ্ধতি ব্যবহার করলে পাবঃ
বাইনারী ১০ এর দশমিক প্রকাশ হলোঃ ২।
এবং বাইনারি ১০ এর অনুসারে মোমবাতিও ২টি রয়েছে।
তাহলে কেকটি বাইনারিতে ১০ অর্থাৎ দশমিকে ২ বছরের বাচ্চাটি পাবে।
বাইনারি প্রকাশ ব্যবহার করে বর্ণের জন্যে কোড
শিখন প্রশ্নঃ ‘MATHEMATICS’, ‘BINARY’, RAMANUJAN এই শব্দগুলিকে বাইনারি কোডে রুপান্তরিত করার চেষ্টা করো।
সমাধানঃ
ইংরেজি বর্ণগুলোর সিরিয়াল নিন্মরুপঃ
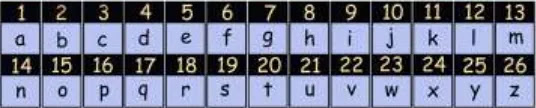
এবং বর্ণমালার কোড নির্ণয়ের জন্য কার্ডের ডট পদ্ধতি নিন্মরুপঃ
| • • • • • • • •• • • • • • • • | • • • • • • • • | • • • • | • • | • |
| 16 | 8 | 4 | 2 | 1 |
এখন, MATHEMATICS এর বাইনারি কোডে রুপান্তরঃ
M=13 এর বাইনারি কোড = 01101
A=1 এর বাইনারি কোড = 00001
T=20 এর বাইনারি কোড = 10100
H=8 এর বাইনারি কোড = 01000
E=5 এর বাইনারি কোড = 00101
I=9 এর বাইনারি কোড = 01001
C=3 এর বাইনারি কোড = 00011
S=19 এর বাইনারি কোড = 10011
তাহলে, MATHEMATICS এর বাইনারি কোড = 0110100001101000100000101011010000110100010010001110011
আবার,
BINARY এর বাইনারি কোডে রুপান্তরঃ
B = 2 এর বাইনারি কোড = 00010
I = 9 এর বাইনারি কোড = 01001
N = 14 এর বাইনারি কোড = 01110
A = 1 এর বাইনারি কোড = 00001
R = 18 এর বাইনারি কোড = 10010
Y = 25 এর বাইনারি কোড = 11001
তাহলে, BINARY এর বাইনারি
কোড = 000100100101110000011001011001
RAMANUJAN এর বাইনারি কোডে রুপান্তরঃ
R = 18 এর বাইনারি কোড = 10010
A = 1 এর বাইনারি কোড = 00001
M = 13 এর বাইনারি কোড = 01101
N = 14 এর বাইনারি কোড = 01110
U = 21 এর বাইনারি কোড = 10101
J = 10 এর বাইনারি কোড = 01010
তাহলে, RAMANUJAN এর বাইনারি
কোড = 100100000101101000010111010101010100000101110
একক কাজঃ
৫ বিট বাইনারি ব্যবহার করে একটি মালা বানাও।
সমাধানঃ
সবুজ বড় গুটিকে বাইনারির ১ ও হলুদ ছোট গুটিকে বাইনারির ০ ধরে বাইনারির ৫ বিট ব্যবহার করে নিচের ছবির মালাটি বানালাম। এক্ষেত্রে বাইনারির হিসাবটি হলোঃ ১০১০০ ০০০০১ ০১০০০

জীবন বাঁচাতে বাইনারি
প্রশ্নঃ দীপু একটি ডিপার্টমেন্টা ল স্টোরের উপরের তলায় আটকা পড়েছে। সে কি করতে পারে ভাবছে? সে সাহায্যের জন্য চিৎকার করে ডাকছে কিন্তু আশেপাশে কেউ নিই। রাস্তার ওপারে সে দেখতে পায় একজন মানুষ কম্পিউটার নিয়ে গভীর রাত পর্যন্ত কাজ করছে। যেহেতু কম্পিউটারে ভাষা বাইনারি তাই দীপু আলো জ্বালিয়ে ও নিভিয়ে বাইনারি কোড দিয়ে সেই মানুষটিকে বুঝানোর চেষ্টা করলো। বলতো জানালায় দীপু কী লিখেছিল?

সমাধানঃ
দীপু জানালায় আলো জ্বালিয়ে ও নিভিয়ে ৫ বিটের কিছু বাইনারি কোড লিখল যেগুলো অন অফ হিসাব করে পাই,
০১০০০ যার দশমিক প্রকাশ হলোঃ ৮
০০১০১ যার দশমিক প্রকাশ হলোঃ ৪+১ = ৫
০১১০০ যার দশমিক প্রকাশ হলোঃ ৮+৪ = ১২
১০০০০ যার দশমিক প্রকাশ হলোঃ ১৬
০০০০০ যার দশমিক প্রকাশ হলোঃ ০
০১০০১ যার দশমিক প্রকাশ হলোঃ ৯
০১১০১ যার দশমিক প্রকাশ হলোঃ ৮+৪+১ = ১৩
০০০০০ যার দশমিক প্রকাশ হলোঃ ০
১০১০০ যার দশমিক প্রকাশ হলোঃ ১৬+৪ = ২০
১০০১০ যার দশমিক প্রকাশ হলোঃ ১৬ + ২ = ১৮
০০০০১ যার দশমিক প্রকাশ হলোঃ ১
১০০০০ যার দশমিক প্রকাশ হলোঃ ১৬
১০০০০ যার দশমিক প্রকাশ হলোঃ ১৬
০০১০১ যার দশমিক প্রকাশ হলোঃ ৪+১ = ৫
০০১০০ যার দশমিক প্রকাশ হলোঃ ৪
এখন, a=1, b = 2, …….z=26 ধরে উপরে প্রাপ্ত দশমিক সংখ্যাকে প্রকাশ করলে পাই,
৮ = h
৫ = e
১২ = l
১৬ = p
০ = Not Appplicable
৯ = i
১৩ = m
০ = Not Appplicable
২০ = t
১৮ = r
১ = a
১৬ = p
১৬ = p
৫ = e
৪ = d
অর্থাৎ, দ্বীপু জানালায় লিখেছিল help i’m trapped.
পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇
👉 চলো বৃত্ত চিনি – ৮ম অধ্যায় – সমাধান | গণিত | সপ্তম শ্রেণী | Class 7 Math Chapter 8 | BD 2023

