
এই পোস্টে আমরা জানব ৭ম শ্রেনীর, বিষয় গণিত এর দ্বিতীয় অধ্যায় বীজগাণিতিক রাশির সূচক, গুণ ও তাদের প্রয়োগ (৫৩ – ৫৮ পৃষ্ঠা ), সম্পর্কে।
দ্বিপদী রাশির বর্গ
একক কাজঃ ছবির সাহায্যে বর্গ নির্ণয় করো।
1. m+n
2. 4x+3
3. 3x+4y
4. 105
5. 99
সমাধানঃ
(1) ছবির সাহায্যে m+n এর বর্গ নির্ণয়ঃ
(i) m+n এর বর্গ অর্থাৎ (m+n)2 নির্ণয়ের জন্য একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য m+n.
(ii) এখন m+n বাহুতে m ও n এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।

(iii) ক্ষেত্রগুলো কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (m+n)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = m2 + 2mn + n2
অতএব, (m+n)2 = m2 + 2mn + n2
(2) ছবির সাহায্যে 4x+3 এর বর্গ নির্ণয়ঃ
(i) 4x+3 এর বর্গ অর্থাৎ (4x+3)2 নির্ণয়ের জন্য একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য 4x+3.
(ii) এখন 4x+3 বাহুতে 4x ও 3 এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।
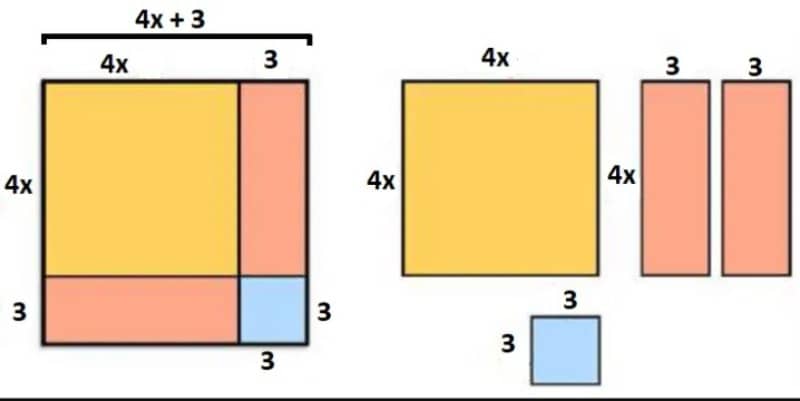
(iii) ক্ষেত্রগুলো কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (4x+3)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = (4x)2 + 4x.3+4x.3 + 32 = 16x2 + 12x +12x + 9 = 16x2 + 24x + 9
অতএব, (4x+3)2 = 16x2 + 24x + 9
(3) ছবির সাহায্যে 3x+4y এর বর্গ নির্ণয়ঃ
(i) 3x+4y এর বর্গ অর্থাৎ (3x+4y)2 নির্ণয়ের জন্য একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য 3x+4y.
(ii) এখন 3x+4y বাহুতে 3x ও 4y এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।

(iii) ক্ষেত্রগুলো কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (3x+4y)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = (3x)2 + 3x.4y+3x.4y + (4y)2 = 9x2 + 12xy +12xy + 16y2 = 9x2 + 24xy + 16y2
অতএব, (3x+4y)2 = 9x2 + 24xy + 16y2
(4) ছবির সাহায্যে 105 এর বর্গ নির্ণয়ঃ
(i) 105 এর বর্গ অর্থাৎ (105)2 নির্ণয়ের জন্য একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য 105.
(ii) এখন 105 দৈর্ঘ্যের বাহুতে 100 ও 5 এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।
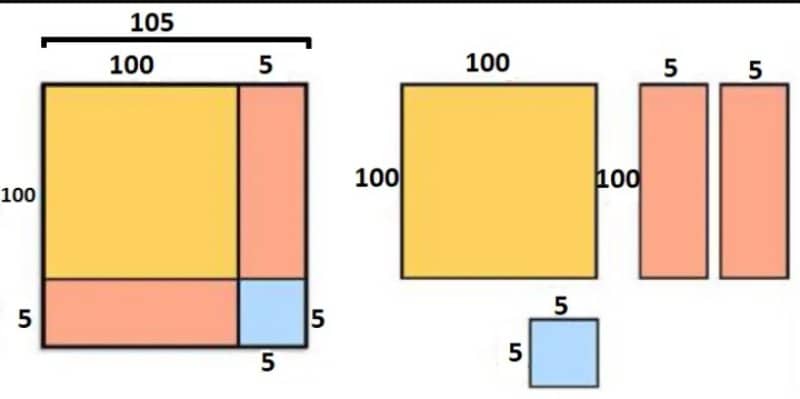
(iii) ক্ষেত্রগুলো কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (105)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = (100)2 + 100.5+100.5 + (5)2 = 10000 + 500 +500 + 25 = 11025
অতএব, (105)2 = 11025
(5) ছবির সাহায্যে 99 এর বর্গ নির্ণয়ঃ
(i) 99 এর বর্গ অর্থাৎ (99)2 নির্ণয়ের জন্য একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য 99.
(ii) এখন 99 দৈর্ঘ্যের বাহুতে 90 ও 9 এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।
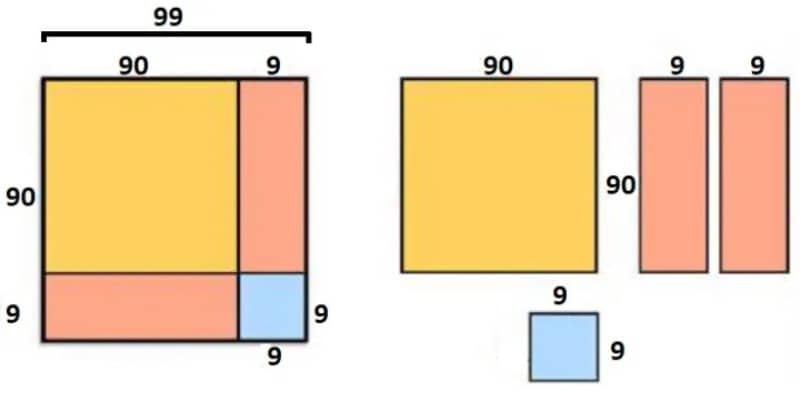
(iii) ক্ষেত্রগুলো কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (99)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = (90)2 + 90.9+90.9 + (9)2 = 8100 + 810 +810 + 81 = 9801
অতএব, (99)2 = 9801
কাগজ কেটে প্রমাণ করোঃ a2+b2 = (a+b)2 – 2ab
সমাধানঃ
(i) একটি বর্গাকৃতির কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য a+b এর সমান হয়।
(ii) এখন (a+b) দৈর্ঘ্যের বাহুতে a ও b এর দৈর্ঘ্য চিত্র অনুসারে চিহ্নিত করি। ফলে চারটি ক্ষেত্র পাওয়া গেল।

(iii) ক্ষেত্রগুলো কাগজ হতে কেটে আলাদা করি এবং প্রতিটি ক্ষেত্রের ক্ষেত্রফল নির্ণয় করে যোগ করি। ফলে (a+b)2 পাওয়া গেল।
প্রাপ্ত ক্ষেত্রফল = (a)2 + ab + ab + (b)2 = a2 + 2ab + b2
তাহলে,
(a+b)2 = a2 + 2ab + b2
বা, a2 + 2ab + b2 = (a+b)2
বা, a2+ b2 = (a+b)2 – 2ab [প্রমাণিত]
সহজ উপায়ে (বীজগণিতের সূত্র) বর্গসংখ্যা নির্ণয়:
কাজঃ সহজ উপায়ে 52, 71, 21, 103 এর বর্গ নির্ণয় করো।
সমাধানঃ
52 এর বর্গ
= 522
= (50+2)2
= 502+2.50.2+22 [সূত্রানুসারে]
= 2500 + 200 + 4
= 2704
71 এর বর্গ
= 712
= (70+1)2
= 702+2.70.1+12 [সূত্রানুসারে]
= 4900 + 140 + 1
= 5041
21 এর বর্গ
= 212
= (20+1)2
= 202+2.20.1+12 [সূত্রানুসারে]
= 400 + 40 + 1
= 441
103 এর বর্গ
= 1032
= (100+3)2
= 1002 + 2.100.3 + 32 [সূত্রানুসারে]
= 10000 + 600 + 9
= 10609
ছক ১.২ সহজ উপায়ে বর্গসংখ্যা নির্ণয় করে পূরণ করো।
সমাধানঃ
| সংখ্যা | বর্গসংখ্যা | সংখ্যা | বর্গসংখ্যা |
| 1 | 1 | 11 | 121 |
| 2 | 4 | 12 | 144 |
| 3 | 9 | 13 | 169 |
| 4 | 16 | 14 | 196 |
| 5 | 25 | 15 | 225 |
| 6 | 36 | 16 | 256 |
| 7 | 49 | 17 | 289 |
| 8 | 64 | 18 | 324 |
| 9 | 81 | 19 | 364 |
| 10 | 100 | 20 | 400 |
কাজঃ সারণিভূক্ত বর্গ সংখ্যাগুলোর এককের ঘরের অঙ্কগুলো ভালোভাবে পর্যবেক্ষণ করে কোন মিল খজেুঁ পেলে কিনা দেখ।
সমাধানঃ
সারণিভূক্ত বর্গ সংখ্যাগুলোর এককের ঘরের অঙ্কগুলো ভালোভাবে পর্যবেক্ষণ করে একটা মিল খুকে পেয়েছি যা হলোঃ বর্গ সংখ্যা গুলোর এককের ঘরে 0, 1, 4, 5, 6 অথবা 9 অংকটি রয়েছে।
কাজঃ
১। কোনো সংখ্যার একক স্থানীয় অঙ্ক কত হলে সংখ্যাটি বর্গসংখ্যা হতে পারে?
সমাধানঃ
কোন সংখ্যার একক স্থানীয় অঙ্ক 0, 1, 4, 5, 6 অথবা 9 হলে সংখ্যাটি বর্গ সংখ্যা হতে পারে।
২। পাঁচটি সংখ্যা লেখ যার একক স্থানের অঙ্ক দেখেই তা বর্গসংখ্যা নয় বলে সিদ্ধান্ত নেওয়া যায়।
সমাধানঃ
কোন সংখ্যার একক স্থানের অঙ্ক দেখেই তা বর্গসংখ্যা নয় বলে সিদ্ধান্ত নেওয়া যায় এমন পাঁচটি সংখ্যা হলোঃ
12, 17, 22, 33, 43
একক কাজঃ উপরের মতো ছবির সাহায্যে বর্গ নির্ণয় করো।
1. (m+n)
2. (4x+3)
3. (3x+4y)
4. 95
5. 99
সমাধানঃ
1 – 3 পর্যন্ত সমাধান পূর্বেই করা হয়েছে। 4 – 5 এর সমাধান নিচে দেয়া হলো। [উল্লেখ্যঃ নিচের পদ্ধতিতে (a-b)2 কাঠামোর যেকোন সমাধান কাগজ কেটে তোমরা করতে পারবে।]
4. 95
(i) যেকোন একটি বর্গাকৃতির কাগজ কেটে নিই যার প্রতি বাহুর দৈর্ঘ্য 100 এর সমান ধরি।
(ii) নিচের চিত্রের মত 100 দৈর্ঘ্যের বাহুকে 95 ও 5 দৈর্ঘ্যে চিহ্নিত করি।
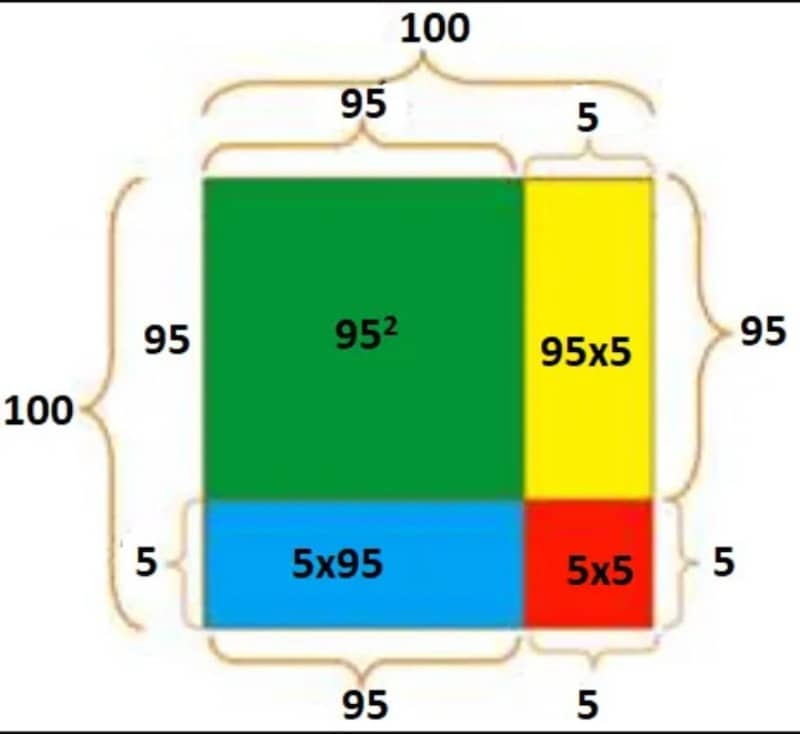
(iii) এখন, চিত্র অনুসারে সবুজ বর্গের ক্ষেত্রফল = সমগ্র বর্গের ক্ষেত্রফল- [হলুদ আয়তের ক্ষেত্রফল+ লাল বর্গের ক্ষেত্রফল + নীল আয়তের ক্ষেত্রফল] অর্থা ৎ,
952 = 1002 – [95×5+5×95+5×5]
বা, 952 = 10000 – [475+475+25]
বা, 952 = 10000 – 975
বা, 952 = 9025
অতএব, 95 এর বর্গ 9025
5. 99
(i) যেকোন একটি বর্গাকৃতির কাগজ কেটে নিই যার প্রতি বাহুর দৈর্ঘ্য 100 এর সমান ধরি।
(ii) নিচের চিত্রের মত 100 দৈর্ঘ্যের বাহুকে 99 ও 1 দৈর্ঘ্যে চিহ্নিত করি।
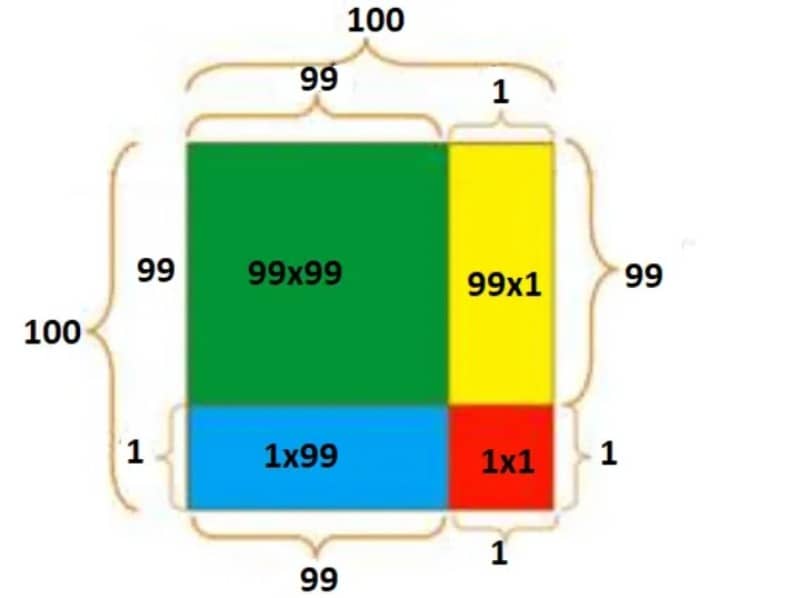
(iii) এখন, চিত্র অনুসারে সবুজ বর্গের ক্ষেত্রফল = সমগ্র বর্গের ক্ষেত্রফল- [হলুদ আয়তের ক্ষেত্রফল+ লাল বর্গের ক্ষেত্রফল + নীল আয়তের ক্ষেত্রফল] অর্থা ৎ,
992 = 1002 – [99×1+1×99+1×1]
বা, 992 = 10000 – [99+99+1]
বা, 992 = 10000 – 199
বা, 992 = 9801
অতএব, 99 এর বর্গ 9801
ত্রিপদী রাশির বর্গ
কাজঃ (a+b+c)2 এর বর্গ কাগজ কেটে নির্ণয় করো।
সমাধানঃ
(i) কাগজ কেটে একটি বর্গ নিই যার প্রতি বাহুর দৈর্ঘ্য a+b+c এর সমান।
(ii) এখন, a+b+c বাহুতে b ও c এর দৈর্ঘ্য নিচের চিত্র অনুসারে চিহ্নিত করি ফলে সম্পূর্ণ বর্গটি ৯টি ক্ষুদ্র ক্ষেত্রে বিভক্ত হলো।
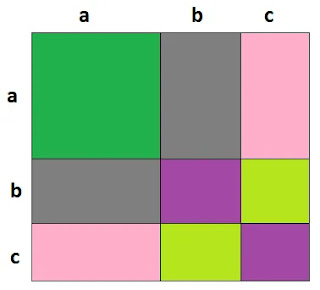
(iii) এখন সম্পূর্ণ বর্গের ক্ষেত্রফল = (a+b+c)2
তাহলে, চিত্র অনুসারে,
(a+b+c)2
= 9 টি আয়তক্ষেত্রের ক্ষেত্রফল
= a2 + ab + ac + ab + b2 + bc + ac + bc + c2
= a2+b2+c2 + 2ab + 2bc + 2ca
= a2+b2+c2 + 2(ab+bc+ca)
একক কাজঃ নিচের সমস্যাটি কাগজ কেটে বা ছবি এঁকে সমাধান করো।
(2x+3y+4z) এর বর্গ নির্ণয় করো।
সমাধানঃ
কাগজ কেটে একটি বর্গাকার কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য (2x+3y+4z) এর সমান হয়।
এখন, (2x+3y+4z) দৈর্ঘ্যের বাহুতে 3y ও 4z দৈর্ঘ্যকে নিচের চিত্র অনুসারে চিহ্নিত করি। ফলে ৯টি আয়তক্ষেত্র পাওয়া গেল।
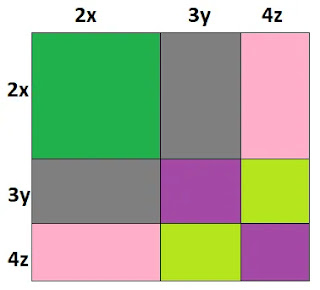
আয়ত ক্ষেত্রগুলোর ক্ষেত্রফল এর সমষ্টি প্রত্যেকটির দৈর্ঘ্য ও প্রস্থ অনুসারে নিন্মরুপঃ
2x.2x+2x.3y+2x.4z+2x.3y+3y.3y+3y.4z+2x.4z+3y.4z+4z.4z
= (2x)2+6xy+8xz+6xy+(3y)2+12yz+8zx+12yz+(4z)2
= 4x2+9y2+16z2+12xy+16zx+24yz
এখন, সম্পূর্ণ বর্গের ক্ষেত্রফল = (2x+3y+4z)2
তাহলে,
(2x+3y+4z) এর বর্গ 4x2+9y2+16z2+12xy+16zx+24yz
একক কাজঃ
১) কাগজ কেটে নিচের রাশিগুলোর বর্গ নির্ণয় করে শিক্ষকের কাছে জমা দাও।
1. a+3
2. 3x-5
3. 999
4. 2x+y+3z
সমাধানঃ
1. a+3
কাগজ কেটে (a+3) এর বর্গ নির্ণয়ঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও 3 এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
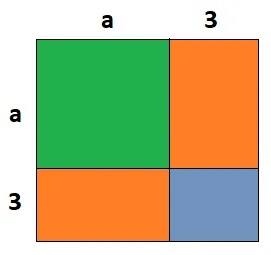
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
বর্গাকৃতি কাগজের ক্ষেত্রফল = 4 টি ক্ষেত্রের ক্ষেত্রফল
বা, (a+3)2 = a.a+a.3+a.3+3.3
বা, (a+3)2 = a2+3a+3a+32
বা, (a+3)2 = a2+6a+9
অতএব, (a+3) এর বর্গ = a2+6a+9
2. 3x-5
কাগজ কেটে (3x-5) এর বর্গ নির্ণয়ঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 3x-5 ও 5 এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
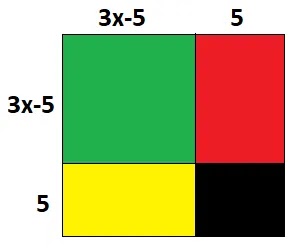
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (3x-5)2 = (3x-5+5)2 – [(3x-5)5+5(3x-5)+5.5]
বা, (3x-5)2 = (3x)2 – [15x-25 +15x -25 + 25]
বা, (3x-5)2 = 9x2 – [30x-25]
বা, (3x-5)2 = 9x2 – 30x + 25
অতএব, (3x-5)2 এর বর্গ = 9x2 – 30x + 25
3. 999
কাগজ কেটে 999 এর বর্গ নির্ণয়ঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 1000-1 ও 1 এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
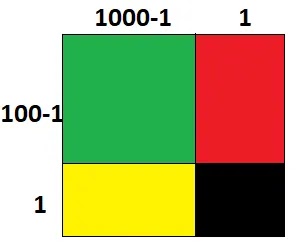
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (1000-1)2 = (1000-1+1)2 – [(1000-1)1+1(1000-1)+1.1]
বা, 9992 = (1000)2 – [1000-1 +1000 -1 + 1]
বা, 9992 = 1000000– 1999
বা, 9992 = 998001
অতএব, 9992 এর বর্গ = 998001
4. 2x+y+3z
কাগজ কেটে (2x+y+3z) এর বর্গ নির্ণয়ঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 2x, y ও 3z এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
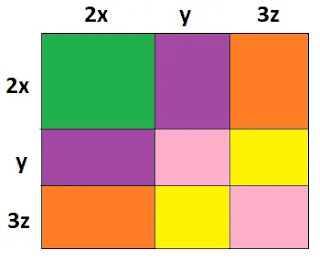
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 9 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
বর্গাকৃতি কাগজের ক্ষেত্রফল = 9 টি ক্ষেত্রের ক্ষেত্রফল
বা, (2x+y+3z)2 = (2x)2+2xy+6zx+2xy+y2+3yz+6zx+3yz+(3z)2
বা, (2x+y+3z)2 = 4x2+y2+9z2+4xy+12zx+6yz
অতএব, (2x+y+3z) এর বর্গ = 4x2+y2+9z2+4xy+12zx+6yz
২) কাগজ কেটে প্রমাণ করো।
1. a2 +b2 = (a-b)2 + 2ab
সমাধানঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
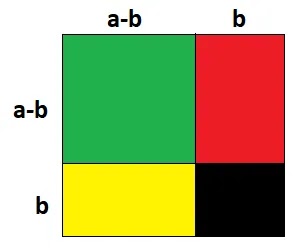
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা, (a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা, (a-b)2 = a2 – [2ab-b2]
বা, (a-b)2 = a2 – 2ab + b2
বা, (a-b)2 + 2ab = a2 + b2 [পক্ষান্তর করে]
বা, a2 + b2 = (a-b)2 + 2ab [প্রমাণিত]
2. (a-b)2 = (a+b)2 – 4ab
সমাধানঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
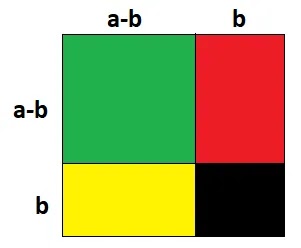
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা, (a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা, (a-b)2 = a2 – [2ab-b2]
বা, (a-b)2 = a2+ b2 – 2ab ……..(i)
আবার,
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
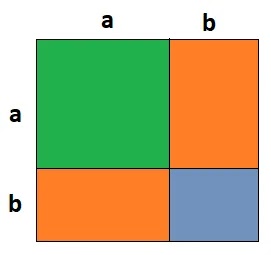
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সম্পূর্ণ বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা, (a+b)2=a2+b2+2ab ………(i)
আবার,
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
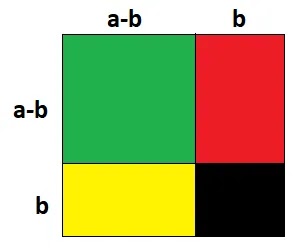
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা, (a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা, (a-b)2 = a2 – [2ab-b2]
বা, (a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i) – (ii) করে পাই,
(a+b)2-(a-b)2=a2+b2+2ab – (a2+ b2 – 2ab)
বা, (a+b)2-(a-b)2=a2+b2+2ab – a2– b2 + 2ab
বা, (a+b)2-(a-b)2=4ab
বা, (a+b)2=(a-b)2+4ab [প্রমাণিত]
4. (a+b)2 + (a-b)2 = 2(a2 +b2)
সমাধানঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
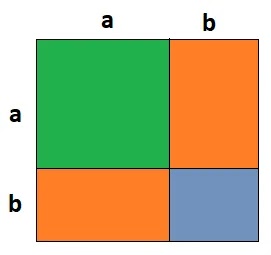
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সম্পূর্ণ বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা, (a+b)2=a2+b2+2ab ………(i)
আবার,
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
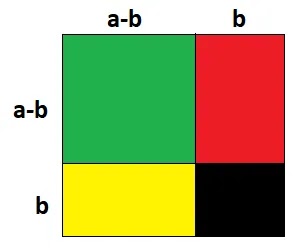
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা, (a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা, (a-b)2 = a2 – [2ab-b2]
বা, (a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i) + (ii) করে পাই,
(a+b)2+(a-b)2 =a2+b2+2ab + a2+ b2 – 2ab
বা, (a+b)2+(a-b)2=2a2+2b2
বা, (a+b)2+(a-b)2=2(a2+b2) [প্রমাণিত]
5. (a+b)2 – (a-b)2 = 4ab
সমাধানঃ
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
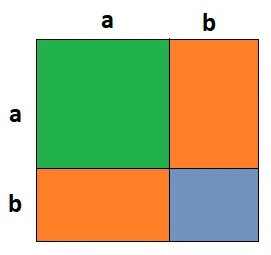
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সম্পূর্ণ বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা, (a+b)2=a2+b2+2ab ………(i)
আবার,
(i) প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত করি।
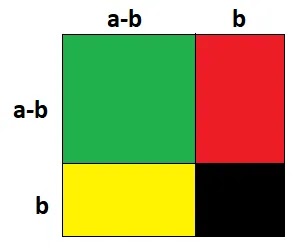
(ii) তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii) এখন, চিত্র অনুসারে,
সবুজ অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা, (a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা, (a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা, (a-b)2 = a2 – [2ab-b2]
বা, (a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i) – (ii) করে পাই,
(a+b)2-(a-b)2=a2+b2+2ab – (a2+ b2 – 2ab)
বা, (a+b)2-(a-b)2=a2+b2+2ab – a2– b2 + 2ab
বা, (a+b)2-(a-b)2=4ab [প্রমাণিত]
পরবর্তী অধ্যায়ের সমাধান পেতে নিচের লিংকে ক্লিক করুন 👇

